The name's Overun. Rise Overun. But you can call me Slope.

The year ended with a great assembly. The dance classes performed their jazz dance final, complete with white gloves and top hats. The group of students working with local "guerilla-style theater" group headRush performed their one act play that they put together; the play focused on Mexican immigrants coming to the US for a better life, and the difficulties they encounter, along with the next generation's difficulties in dealing with gangs. The student body loved the play and quite a few of the teachers ended up with wet eyes (as one of the "actors" told us later, the DCP staff is too sensitive). The students working with headRush loved their experience and have decided to keep the project going, even though headRush's fellowship with Montalvo (where they are currently artists-in-residence) is coming to a close. The new theater company will be known as "Teatro Lobos Unidos" (I think I may be their club advisor). Finally, the world-famous Numeracy Project made our yearly debut (Rise Overun is my stage name) with Back in SSR, Equis Cuadrada, and Honor Roll-a.

On the last day of school, students were totally high on the promise of sweet freedom that lay just around the corner (so was the staff, to be quite honest). The day went pretty well, though students got more and more restless throughout the day. For me, the kids I taught during the last period before break was my honors Algebra 2 class. I was interested to see how these students would behave. They actually did spend most of the period getting their work done. I knew lecture would be a waste, so I had them work on a packet to practice graphing parabolas; they had to graph the absolute value of quadratic functions; graph quadratic inequalities; and solve quadratic inequalities graphically. They did pretty well, but some of them looked like they were about to explode out of their skin. Toward the end, when I was trying to get their attention to explain the homework and what would happen when they got back from break, one of the students wouldn't sit down. I asked the class what would happen to him if he made me keep them past the bell. It didn't take long for him to sit down after that!

One other thing: presents. On the last day of school, there are always students who bring in Christmas presents for their teachers. Only a few students in high school still do this (I assume many more do in elementary school). The spirit behind this is really touching. Our families don't have to get us anything, and many don't have the budget for extra expenses. The presents are usually little trinkets like a box of candy or a bottle of hand lotion. This year, I received a few boxes of candy (the staff room is always piled high with open candy boxes during this time of year). One student gave me a mug filled with marshmallows (other staff later had to explain to me that it was a hot-cocoa making kit!). But my most interesting gift was from the student who gave me a plaid golf scarf and a set of XL men's thermal long underwear. A bit odd, but very sweet.

The year is over, but not the semester. When we get back from break, there will be a week of classes for review, and then final exams. I didn't get to finish my current unit, so I think I will actually have to give the unit test in the second semester, after the final exam. That will be a bit odd, but I haven't gotten the chance to teach students completing the square yet, and I think I can't chop that out.

I'm out of town now, visiting family in Cleveland and then St. Louis, and I probably won't be posting much more until the beginning of January. Happy holidays!

Showdown!

I forgot to post about the last lesson - I gave students a quiz on radicals and complex numbers, and I also taught them how to factor trinomials in the form ax^2 + bx + c when the gcf = 1. I graded the quizzes over the weekend, and they weren't that great, so I decided to spend today reviewing with them.

So after reviewing the homework carefully, we spent the rest of the class doing an activity called "Showdown". I got this from another teacher, and I'm not sure where he got it from. When managed properly, I find that this activity works extremely well for review. Students always want to know if it's a competition, and it's not - it's a collaborative activity. Though competitions are fun and have their place, they often lead to one student in the group doing all the work so that the team can get the highest score. This activity helps students communicate with each other and lets them go at their own pace. I made a set of 16 problem cards (with answers on the back) for each group, which I'll post on ILoveMath. Here is the overhead of the rules I made for the class:

Showdown Setup:

• Each group selects a team captain who will set the pace of work.


• Each student needs a handful of answer slips (there are 16 problems in total).


• Each group needs a team answer sheet.

Process:

1. The captain shows problem 1. All team members work individually and silently on the problem. Write answers on answer slips, turning them upside-down when done (or totally stuck).


2. When the captain sees all slips are upside-down, he/she calls “Showdown”. Group members show and compare their answers, explain their work, and come up with a group answer. The captain writes the group answer on the team answer sheet.


3. The captain turns the problem card over and compares the given answer to the team’s answer. If the answers are different, discuss. At this point, you can ask me for help if you can’t figure out how to get the answer.


4. Move on to the next problem and repeat.

The individual time gives students a chance to access their own knowledge. The group time gives students a structured way to collaborate, and it also prevents them from asking me for help before they have thoroughly discussed a problem. I am freed up to be able to walk around and see what's happening, listen to their discussions, and point things out to them when needed. I've done this activity in the past where it did not work exactly as it's supposed to (i.e. students start collaborating right away, or they look at the answer right away), but my class today did an outstanding job with it.

The Numeracy Project

To complete the dorky math teacher persona, I am in a band with some other teachers (and a couple of students). We are called The Numeracy Project, and we so rock! The other teachers in the band are actually quite good; I just strum rhythm guitar and look goofy. Sometimes we write our own songs (Wednesday, we are debuting an A. Malizia original: "Equis Cuadrada"), but mostly we take existing songs and rewrite the words. Old favorites: Sweet Home Alameda (Sweet Home Alabama); Honor Roll-a (My Sharona); My Graduation (My Generation); you get the picture. I have finally put pen to paper to try my own skills as a composer. What do you think? (The tortoise and hare is a reference to an activity done at the beginning of the slope unit.)

Slope is Rise Over Run (sung to House of the Rising Sun, by The Animals)

There is a ratio in my math class,
(they call it Algebra 1),
and it’s been the ruin of many a freshman.
For reals, it’s hella not fun!

My mind is always wandering,
the hare and tortoise run.
The teacher points, and then declares,
slope is rise over run.

The change in Y, the change in X,
the stupid race is won.
And the only answer that’s required is
slope is rise over run.

Organ Solo

Oh seniors, help the freshmen
not to do what I have done.
I wasted my time in office hours,
pretending to get homework done.

Well, I open up my textbook,
I wipe away the drool.
I’m ready to do whatever it takes
to not go to summer school.

There is a ratio in my math class,
(they call it Algebra 1).
Though it’s been the ruin of many a freshman,
now, I’m no longer one.

Financial Literacy Project (or, screwing over the freshmen for fun and profit!)

I have the beginnings of an idea for a project to do later in Spring, for the exponential functions unit, in conjunction with our freshman College Readiness classes.

I was thinking about when I was a freshman in college, and how there were always tables set up by credit card companies who would attract crowds of freshmen with such irresistable items as Citibank t-shirts and Bank of America frisbees. They would give a credit card to just about anyone. There have been lots of reports about how so many college students get into incredible credit card debts because they don't know how to manage a credit card, and they are preyed on by these vultures.

I would like to run a simulation, where my Algebra 2 students run their own credit card companies. We will examine what interest means, and the types of predatory practices credit card companies engage in (i.e. a low introductory rate that suddenly changes for various reasons, allowing very low monthly payments, etc.). Then, the students will design their own cards and draw up a credit card offer. They will then set up booths in the school one day, and the freshman College Readiness students will be asked to sign up for at least one card (my students will need to come up with ways to attract their business with their own exciting promotional items... I'm predicting free bags of hot cheetos and the like).

Then, for the next few weeks, in the College Readiness classes (who will be in their Financial Literacy unit), the freshmen will have a given job and salary, mandatory expenses, and optional expenses. They can use their credit card at will, and pay as much of their balance as they choose. To make this more exciting for the students, I'd like to think about how to tie their decisions to real-life consequences (i.e. if you buy an iPod with your credit card, you earn the privilege to listen to one during tutorial time, or if you go on a shopping spree, you earn a free-dress day). Students will be responsible for tracking their budgets and payments.

Then, after a few weeks of the simulation, my students will collect the data and calculate how much the freshmen owe. Whichever credit card company made the most money will get some sort of prize (maybe I'll take them out to lunch or something). Though this may seem counter to the spirit of the project, I'd like to do this for two reasons. One, by thinking of ways to be as deceptive as possible, students will be more attuned to potential deception later when it really counts. Two, they'll enjoy "being bad" (which will increase engagement) and it's a safe environment in which to play the bad guy.

My students will use this simulation as a springboard for the exponential functions unit, compounded interest, and so on. To wrap it up, they will put together a presentation to make at our weekly school assembly where they report on the results of the simulation, explain why we did it, and include a note of caution to all students about the dangers of using credit cards.

The logistics are not thought out yet, but I think this has the potential to be both fun and very educational. Any thoughts?

Next Lesson: Powers of i; Basic Trinomial Factoring

Today in class, we started with a mini-lesson on finding the powers of i, using the "multiplying by i = rotating by 90 degrees about the origin" metaphor. I misjudged - I made it a self-paced worksheet, but it was too complex (no pun intended) for them to handle on their own. When I went over it with them as a class, they started to understand it a lot better, but it ended up taking much more time than I had planned. The circle help students see why the pattern repeats in 4s. If you start at 1 on the real axis, and make a full circle, you will have multiplied by i 4 times. Therefore, any multiple of 4 in the exponent will cause an integral number of circles, landing you back at 1. Then, the remainder indicates how many more rotations you need and where to end up on the complex plane.

I'm at the point in the year where finals are looming and I feel pressed to rush through the curriculum to finish the unit. But what's the point, if they're not going to retain information as I charge ahead? I may need to scale back my learning objectives for this unit, or for the upcoming units.

After the powers of i, I wanted to do a quick review of factoring out the greatest common monomial factor from a polynomial, as well as factoring quadratic trinomials where a = 1. This is basic stuff that they did in algebra 1, but they had forgotten so much of it. By the end of class, most of them were starting to remember having done this before... so I go back to my earlier question about retention. I feel like this is a fundamental algebra 1 concept that should be retained from spring of this year (when they learned it in algebra 1) until now. Maybe going through it again now will help them get it into longer term memory... but how many times do they need to review the same topic until it sinks in?

Instead of giving a worksheet for practice, I wanted to show students how I create factorable trinomials, and for them to create their own and quiz each other. I think that this will be an effective way to help give them a deeper understanding. Unfortunately, we ran out of time because of the earlier problems. I am moving this into tomorrow's lesson, so hopefully it will work out.

Next Lesson: Operations on Complex Numbers

Tomorrow, the Do Now will introduce the idea of finding the distance to the origin on a coordinate plane by creating a right triangle and using the Pythagorean Theorem. Students must calculate the shortest distance from a given point back to the origin, where they left their sweeties, and therefore want to hurry back to.

Following this, I will do direct instruction on addition, subtraction, multiplication, and division. Multiplying by the complex conjugate for division will be a nice follow up to simplifying fractions like 2/(3 + root2) from the previous lessons. Then, we will recall what was learned during the Do Now to understand how to calculate the absolute value of a complex number. Students will plot complex numbers in the complex plane, and then draw a right triangle and calculate the length of the hypotenuse. I will ask students to figure out other complex numbers that have an equal absolute value, and to determine, given a set of complex numbers, which one is farthest from the origin.

Finally, students will have about 20 minutes to work on these types of problems in pairs and ask for help. Not a very exciting lesson, to be sure, but, for some reason, complex numbers and their operations seem to be hit pretty heavily on the STAR test, so it needs a lot of class time. I don't think students will be asked to find the absolute value of a complex number, but it is good scaffolding for the distance formula, which is an indispensable tool in any high school mathematician's bag of tricks.

The lesson will be posted on ILoveMath.

Next Lesson: Intro to Complex Numbers

Still catching up - this was today's lesson...

This lesson's scaffolding is based off of some ideas in the book Where Mathematics Comes From, by George Lakoff. I found this book to be fascinating, as it speaks directly to the question of whether math is a human discovery or a human invention. The book is firmly on the side of invention, explaining how a set of basic "grounding metaphors" create a foundation on which we've built the rest of mathematics. If you're interested in these ideas, I highly recommend reading it. Whether or not you agree with the conclusions, it'll really get you thinking.

In the book, they discuss the metaphor that is used to understand where the imaginary number i comes from. Essentially, you can think of multiplying by -1 on the real number line as a 180 degree rotation. Once you accept this metaphor, then it opens the question: multiplying by what number gives you a 90 degree rotation? If you multiply by that number twice, that means you've rotated 90 degrees twice. Since this is equal to 180 degrees, multiplying by the mystery number twice gives the same result as multiplying by -1. Therefore, the mystery number must be the square root of -1. Whoa. I thought that was an interesting way of looking at it. It allows you to then see why the imaginary axis is perpendicular to the real axis. It also allows you to see why the powers of i follow that 4 number pattern which students need to know. You can go around in a circle, stopping every 90 degrees at an axis. If you start from 1 on the real axis, you'll pass through 1, i, -1, -i, then back to 1. Also, this had an added benefit: one student asked what would happen if you rotate 180 degrees twice. He realized that this would be the same as multiplying by -1 twice. When I pointed out that this rotation would get you back to where you started from, I think his jaw dropped a bit - he may have finally understood a reason that explains why a "negative times a negative is a positive"!



So I designed a handout for students to work through these ideas, we discussed them, and I finished with about 20 minutes of lecture to tie it all together and do some exaxmples. I love this lesson, because I feel like it allows for some deep learning, and the mathematics are not that tough, so almost all students can follow it pretty easily.

This lesson will be posted on ILoveMath.

Next Lesson: Properties of Square Roots

I'm catching up a bit - this was Thursday's lesson...

The homework due for this lesson was a review/exploration of the multiplication and division properties of square roots. During the Do Now, students practiced this. I gave them problems that couldn't be simplified also (i.e. root 3 + 2root 5) because students often confuse the properties and apply them to addition and subtraction as well. They seem to need to hear about it quite a few times before it sinks in.

After this, I did some direct instruction. I started with some historical background on radicals which I just read about recently. The checkmark part of the radical sign is thought to be a manuscript form of the letter "r", which of course stands for "radix", Latin for root. It was first used in the early 1500s. What I didn't know was that the extended top bar is the last remaining holdover of the old notation of grouping, called the vinculum. I decided to explain this to students so they would understand why "you do what's in the radical first", and it actually did seem to click for some of them.

Following this, I showed them how to reduce square roots by finding the prime factorization and pulling out pairs of like factors. Or, as one student recalled from his 8th grade teacher, it's like two convicts trying to escape from jail, where one of them gets out but the other gets shot. I tried to go for a more mathematical explanation... We also looked at rationalizing the denominator, which was new to them. This is a holdover from the days before calculators, when dividing by a radical was quite a chore. But, the concept of rationalizing is very useful in all those fun limit problems in calculus, so I thought we should still go ahead and learn it.

After this, there was pair work practice, with lots of different types of problems combined together, the hardest being simplifying fractions like (5 + root3)/(4 - root6).

I'll post this lesson on ILoveMath.

I'm more afraid of the midterm than they are...

Tomorrow is the fall midterm for my Algebra 2 Honors class. It covers everything from the start of the year: the real number system and its properties, solving equations with rational coefficients, everything about functions and graphical analysis, systems of linear and non-linear inequalities, and 3x3 systems of equations. That's quite a large chunk of material for anyone, let alone students who were below grade level less than 2 years ago.

DCP students are notorious for being able to do well in the short term, but completely falling apart in the long term (>3 weeks or so). Traditionaly, the majority of a class will get a C or an F (no Ds at DCP!) on a midterm or final, even if they had been doing well all along. We haven't figured out yet how to help them do better on large cumulative exams. Sometimes it feels like their brains are a cup that can hold a fixed amount of liquid - as soon as you pour more in, the rest splashes out to make room. For this reason, final exams are only 10% of the class grade in all freshmen classes, and it goes up by 5% a year. We need our seniors to be prepared to take college classes where the final is 25 - 30% (or even more) of the grade, and to understand how significant that is.

I don't know if their retention problems mean that they did not really understand the material in the first place, or if it means that they still don't really understand how to study (or how you need to study differently for this kind of exam), or if there is something else going on. I was helping a student review today, who admittedly has been struggling to do well, but usually has a pretty good sense of what's going on. He got confused on a problem, so I posed a simpler problem (or so I thought...) to try and help him understand. I wrote on the board: if f(x) = x + 2, what is f(3)? He looked at me like he had no idea what I was talking about. Honestly, I am amazed by this. I have no way to explain why he couldn't answer that question. I do have one observation: when students are struggling with one difficult concept, they seem to be unable to access previously learned concepts at the same time, even if they could use that concept well in a different context. Maybe it's like being able to toss and catch different objects individually with no problem, but dropping them all when trying to juggle.

It makes sense to me that students would forget complex formulas or methods over time - this happens to me too. But, if they learned them properly, a little bit of review should bring them right back. However, when students don't recall foundational concepts (I had a calculus student once ask me, while studying for the final, what a derivative was), I don't know how to help them, except to implore them to see me for as much extra help as possible.

So, we'll see tomorrow how it goes. I'm predicting a bloodbath, but I hope they'll defy the trends. If anyone has ideas about how to better prepare students for cumulative tests, please share them in the comments section.

Update:
Here are the scores:

10| 2
9| 7
8| 0 1 5 8 8
7| 1 2 2 2 4 4
6| 2 5 7 8
5| 2 4 5
4| 9
3|
2|
1|

Well, as predicted, the scores were much lower than a typical unit test. At least the majority of the class still passed, and my top student is still getting over 100%! She's an algebra machine.

Next Lesson: 3x3 Systems Word Problems (and Thanksgiving!)

I just finished the class - last period of the last day before Thanksgiving break, right after a special double-length lunch with music, dancing, and staff v. student volleyball and soccer. Given all that, the class went amazingly well. They were wound up at first and were having "focus problems" (my favorite euphamism), but when we got to the competition, they really got down to work. So the lesson..

After reviewing the homework, students did a warm-up of solving word problems with 2x2 systems. They still have trouble with converting from verbal statements to equations for things like "my second number is 3 more than 6 times my first number". To help them through those, I ask them to try a specific numeric example (reducing the level of abstraction by that step seems to help them see the relationship). I say "imagine my number is 10 - what is 3 more than 6 times 10?" They say 63, and then I ask them how they figured that out. That is usually enough to get them to write out the equation.

After this, we worked together on a word problem that uses a 3x3 system as its model. In this example, the last equation was in a different form (where one variable was already isolated), and they saw how substitution would let them create a 2x2 system, instead of just using linear combination as we had been doing. I'm trying to get them to be as flexible as possible in their problem solving; there are different methods, and you should pick the method that applies best to the given problem.

This left about 35 minutes for students to get into groups of 3 and do a word problem relay. Each group got problem 1 to start with; when they solved it, they brought it to the front for me to check. If they were correct, they got problem 2, and so on. There were 4 problems - I told them they'd get 5 bonus homework points if they solved all 4. At this point, most of the students worked really well (except for one chatty group) and most groups got to the third or forth problem, but none solved the forth in time.

For homework, I gave them a review packet for the Midterm, which will be next Tuesday, when they return. You can imagine how excited they were about that! It's five pages long, and I suggested that they do one per day to keep their math brains running.

It was a nice day today overall, and this little break always comes just in time to keep us all (teachers and students) sane and friendly.

Our Gorgeous Department

Click here to see the rest of the staff. Signed 8x10 glossies are available by request!

Next Lesson: 3D Graphing (better than the PS3!)

In this lesson, I will take the class to our computer lab so we can work with the OS X Grapher application. This is the program I've been using to generate all the 2D graphs I give them on worksheets. It can do 3D graphs as well, with nice lighting and rotation. You can even graph implicit functions and relations - I like plugging in random equations to see what kinds of shapes it can make.

We'll start by looking at the 3 axes and see what the planes x, y, and z = 0 look like, as well plotting an ordered triple.


Then, I'll show them what the graph of ax + by + cz = d looks like, and how three planes can intersect at a single point (this being the solution to a 3x3 system of equations).


We'll also look at systems with no solution (i.e. at least two of the planes are parallel) or an infinite number of solutions (all three intersect at the same line).


I think that seeing this will help them visualize 3D graphing much better than me trying to draw it on the board.

During the demonstration, I will be teaching them how to enter functions in to Grapher. After the demonstration, I will put two 3x3 systems on the board. One has a solution and the other doesn't. They must first decide which does by graphing both and determining which has a point of intersection. Once they decide, they must solve the system algebraically, and then plot the solution to see if it falls on the point of intersection of the planes.

After this, we'll go medium-tech (i.e. just using their TIs). I will show them how to use the "stat plot" feature, and we will plot the points (-1, -10), (1, -18), and (5, 14). I will ask them if they can figure out the function of the parabola that passes through those three points. I don't expect them to be able to figure this out on their own, so I will lead them through plugging in the points into the standard form of a quadratic function, which will generate a 3x3 system of equations. We'll solve this together to find that a = 2, b = -4, and c = -16. Graphing the parabola y = 2x^2 - 4x - 16 will confirm the work.

Hopefully there will be time for them to try this on their own as practice. I'll ask them to find the function of the parabola that passes through (-2, 0), (-1, -6), and (3, -10). This is definitely a lot for one lesson, and I've never done this before (our lab is new!), so I'll have to see how it goes.

Real World Applications

What math teacher hasn't heard "when will we use this in real life?" a thousand times already? Typically you hear this when the going gets tough, but sometimes it's asked as a genuine question - not just teacher-baiting. I've posted on this before, and there was quite a bit of response. It's still an open question, obviously, and based on some discussion we had at our staff meeting today, I wanted to approach the question from another angle.

Though students will always be using their numeracy skills, I don't try to convince them that they will be using algebra, geometry, or trig in their "daily lives", because it is simply not true. I do write word problems that use their names and put them in familiar situations, but just because it is fun for them and me - not because I think this will dramatically increase their buy-in and engagement, or their understanding of mathematical concepts. I talk about how math helps you build logical thinking and problem solving skills, but this doesn't help much for the unmotivated students.

The idea we generated today was not to focus on how students might use advanced math concepts in their own daily lives, but to teach them how they are used by professionals in different lines of work. My quadratic functions unit is coming up. Sure, basketballs fly through the air in lovely parabolas, but does that really create a meaningful connection for a kid, even if they love sports? Maybe, but I doubt it. Does a basketball player quickly use x=-b/2a before taking a shot? Instead, what about some applications of quadratic functions that show how they are really used by scientists, engineers, sociologists, astrophysicists, biologists, etc. Maybe a 5 minute, detailed presentation on how headlights and satellite dishes work? It may not connect to students on a personal level, but it could help them see the value math has to society, and why it's worth studying.

So that's my new task: gathering relevant, interesting applications of math concepts that our department can use for each unit in algebra, geometry, trig, and calculus. I have some ideas already, but I would love to hear other people's thoughts on this. Do you think this will be beneficial? Do you know of good resources regarding these questions? Do you have good examples of applications for specific concepts?

Next Lesson: 3x3 Systems of Equations

Up next are those pesky systems of three equations with three variables. We are going to work on solving them by linear combination. I've decided not to cover matrices in this class because of the time it would take to teach it to a level that had any meaning to the students. I also don't think that they have much application up through Calculus (at least, not enough to justify taking time away from some of the other critical topics).

The class will start with a review of 2x2 systems, including systems with no solution or an infinite number of solutions. They will solve these algebraically and graphically; I want to see if they can draw their own conclusions first about what algebraic results like "0 = 3" or "0 = 0" imply graphically.

After this, I'll do direct instruction on these ideas, followed by a demonstration of how to solve a 3x3 system by linear combination. The steps I'll give them:

1. Decide which variable is easiest to eliminate.


2. Eliminate that variable from one pair of equations.


3. Eliminate the same variable from a different pair of equations.


4. Write the resulting equations as a 2x2 system and solve it.
   
   
   
   1. If the 2x2 has 0 or infinitely many solutions, the same is true about the 3x3 and you can stop there.
   
   
   2. See if you can use division to simplify the new equations.


5. Plug in the solutions to one of the original equations and solve for the third variable.


6. Check by plugging in the solution to the other two original equations.

After that, it's just a matter of practice grinding through a few systems. Homework will be more of the same, with a +10 point mega bonus extra credit problem (solving a 4x4 system).

In the following class, we will use the Grapher application in our Mac lab to see the planes that are produced by an equation with x, y, and z, and to understand what an ordered triple means. We will also be able to see how planes can intersect and so forth, and maybe play around with some more 3-D graphing. Grapher is a great application - check it out if you can.

Next Lesson: Systems of Inequalities

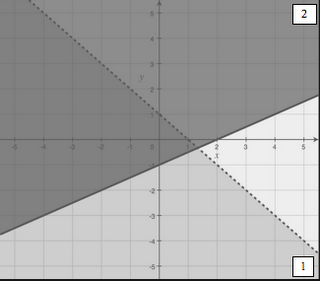
In this lesson, we will go beyond graphing linear inequalities to graphing systems of inequalities, including non-linear inequalities (we'll use absolute value and quadratic equations, as those as the non-linear functions we practiced in the last unit).

Just like in the last lesson, we'll start with a visual activity. Students are given a graph of a system of inequalities, with the two inequalities labeled "1" and "2". They are given a bunch of points, and must determine if the point satisfies the first, the second, both, or neither, and then plot out a "1", "2", "B", or "N" at the coordinates. I want them to not just know that the overlapping region is the solution, but to be able to identify which inequality in the system is not satisfied by a given non-solution point.

At this point, there will be some direct instruction on how to graph a system of inequalities, and reinforcement that the overlapping region is the set of all points that satisfies all inequalities in the system. I will also show them how to graph non-linear inequalities by graphing the "border function" (paying attention to whether it is a solid or dashed line), and then plugging in a test point to determine which region to shade.

After this, students will work independently to practice. I think these will be a bit tough for them because each problem has a little wrinkle in it. I didn't want to give them a bunch of simple lines - that wouldn't be any fun! We'll see how they do. I hope they get it, because I want to move on to the next topic in the following lesson and not spend much time reviewing.

The lesson will be posted at ILoveMath.org.

Next Lesson: Graphing Linear Inequalities

We are finally moving on from the functions unit into a brief unit on systems of equations and inequalities. Last year, I included linear programming in this unit, because it is a great application not just of systems of inequalities, but being able to think critically about a problem, convert verbal information into a mathematical model, and so forth. Unfortunately, I think this topic will be a casualty of going so deep with functions this year. Every time I don't teach some topic, I feel like I am denying them access to ideas that other students will know. Maybe I can squeeze in a one-lesson overview just so they see the idea.

After the unit test, I gave students a homework to review graphing linear functions (horizontal and vertical, slope-intercept, standard form, finding equations of a line, etc.). I think they were happy to get something that was so "easy" for a change.

In this lesson (I actually taught it yesterday), students first were given a Do Now to explore the idea of shading a solution region. I asked them to graph x - 2y = 8. Then, I gave them a bunch of points and the inequality x - 2y < 8, and asked them to algebraically determine if each point was a solution to the inequality. If it was, they had to plot a Y at the coordinates. If not, they had to plot an N. Seeing all the Ys on one side of the line (and on the line itself) and the Ns on the other helped get across the idea of the solution region. Last year, they were taught to shade the solution region in, but I wanted to make sure that they understood what the shading really means. We talked about how the picture would look different if the inequality symbol flipped, or was exclusively greater or less than.

After we established this concept, I just did some direct instruction and showed them how to graph linear inequalities in various forms: x < c; y < c; |x| < c; |y| < c; y < mx + b; ax + by < c. After each example I did, they did a similar example on their own (switching the type of inequality symbol).

The class ended with some individual/pair practice of graphing. The practice also included determining visually if a point is a solution (given the graph), and then confirming this algebraically.

The homework includes more of the same type of practice. It also has a couple of non-linear inequality challenge problems (like y < (x - 3)^2 + 4) to help them work on their synthesis skills.

I'll post the whole lesson on ILoveMath.org

Functional Success

Break out the champagne! Here are the results to the Functions and Relations unit test:

10| 3
9| 0 1 2 3 3 7 7 8 8
8| 0 0 4 8
7| 0 1 7 8 9 9
6| 8
5|
4| 8 8
3|
2|
1|

I'm really happy that they did so well. It's good to have some real successes - both for me and for the students. Of course, now I worry that the test was too easy! I'm posting it at ILoveMath if anyone wants to look at it or use parts of it (or you can email me for a copy). I would love to hear any comments on it, because I redid the whole unit this year, and I strayed quite a bit from the state standards.

I'm really not obsessed with transformers, I promise!

...but this is just too funny. Click in the box to play the video.

November Surprise

Something happened this weekend that I don't think has ever happened in any class in the past 6 years: every student in my 3rd period Algebra 2 regular class passed the unit test. This has happened occasionally on smaller quizzes, but never on a unit test. If you have read enough of my posts to understand what DCP students are like, you'll realize that this is something of a minor miracle. This test was on systems of equations and inequalities, including a word problem and a 3x3 system of equations (with either no solution or an infinite number of solutions). The test wasn't killer, but it definitely wasn't a cakewalk.

I don't usually post about my Algebra 2 regular classes because I don't plan those lessons (we share preps to reduce workload and to ensure that all students learn the same concepts and are assessed the same way). To be honest, because I don't plan the curriculum, I don't spend as much time as I should reflecting on the progress of those classes. But I have some really great kids in those classes too (I got really lucky this year - I have almost no, shall we say, "negative personalities").

Anyway, I told my class the good news today, and I was dead right about the first words that would erupt from the crowd. Say it with me: "Do we get a pizza party?"

The Phantom of the Quinceanera

This weekend, I went to my first quinceanera party. The theme, though I'm not sure why exactly, was Phantom. The birthday girl was a student I had in Numeracy last year, who is a great kid, but has extreme math phobia/anxiety/learning disabilities. She grew comfortable with me as a teacher, and so we were able to have a productive year. Though it is hard to watch a student who works so hard, and is so good natured about everything, struggle so mightily with such basic concepts.

In any case, I was there with about four or five other teachers at the "Reserved for DCP Teachers" table, which was placed up in front, right among the immediate family tables. Both the girl and her mother were very happy that we had come, and it was a great feeling. She was wearing an unbelieveable dress - imagine a relatively small, thin girl stuck in the middle of a 5-foot diameter gold satin gown with ruffles. She told us it made her hips hurt! The 7 damas were wearing gold satin gowns and masks as well, and the 7 male partners were wearing tuxes with gold shirts of some sort, masks, and black capes. There must have been at least 50 other students there - more kept showing up as the night progressed. The party started with food and mariachis playing for a couple of hours. Then, the 15 kids did a couple of choreographed dances to some kind of techno-phantom remix. They left for a costume change and came back to do another dance, and then did another change back into their original dress. Apparently, these dances are choreographed specially for each quinceanera. I've always had students in the past miss class or not get homework done becase they had "quinceanera practice". Now I understand a lot better what kind of work actually goes into making this happen.

Overall, it was a lot of fun. All the students came up to us and shook hands, gave hugs, and were genuinely happy to see us and talk with us. A couple of my Algebra 2 honors students saw me and told me they were getting together later this weekend at the library to study for the test! I even got to see a bunch of former students who have either graduated, or ended up not staying at DCP. This kind of welcoming, community spirit is not only great to be part of - it's really interesting to me... thinking back to my Bar Mitzvah (which is really a very similar event, when it comes down to it), my friends and I would not have been quite so happy to see our teachers there. It would have felt weird, and I definitely would not have run up to my math teacher and given her a hug. No matter how rough our classes are at times, or what type of discipline problems we deal with at school, I'm always amazed by how connected our students and their families are to us, to the school, and to each other.

Update:
At school today, students kept coming up to us and asking why we left the party so early. They wanted to dance with us!

Next Lesson: Quiz 3 and Study Groups

The previous lesson on solving equations and inequalities graphically was very difficult for the students, and I ended up having to do an entire extra lesson of just practice. They worked very hard and I heard quite a few "my head hurts!" comments. Even with that effort, they were taking much longer than I had predicted to do the work, so I ended up pushing the quiz off until the next lesson (this afternoon).

It's interesting: my students are easily able to solve equations such as 2|3x - 4| + 5 = 9 this way, by identifying points of intersection of the functions f(x) = 2|3x - 4| + 5 and g(x) = 9, and looking at their x-values.

As soon as the problem changes to an inequality like 2|3x - 4| + 5 > 9 , they get lost. There seems to be a disconnect between knowing where the f(x) values are greater than the g(x) values (which they understand), and being able to identify the set of x-values that produce those y-values. Many of the students seem to flip back and forth between the x- and y-values and get confused with what they are doing.

In the review lesson, I had them start again with writing the solution in inequality and interval notations when given a number line. This seems to have helped some of them make the connection. I think that many more students were getting the idea by the end of class. I'll see how much they have actually learned when I grade the quizzes today.

After the quiz, they will be working in study groups, which is one of my goals for this year. Part of their homework for today was to look at the different sections that will be on the test (which I listed for them), to flip through notes and old quizzes to remember what types of problems are in each section, and then to rank those sections based on how well they think they are prepared. I resisted creating a review packet for them for when they will be working in their study groups today. Instead, they must compare their rankings and decide as a group what topics to study. Then, they need to find example problems in their notes, homework, and old quizzes. This is risky, because students (even my lovely honors kids) without a concrete assignment (like a worksheet) tend to lose focus and not use their time well. But that is what I want to coach them on, so we'll see. I did make a short review sheet with some key problems for them to complete as homework. I hope to take away more of this scaffolding by the end of the year.

Here are the sections on the Unit 2 Test:

1) Functions and relations

2) Function notation & function composition

3) Representational fluency (using equations, tables, arrow maps, and graphs)

4) Operations on functions (adding, subtracting, multiplying)

5) Domain and range

6) Piecewise functions

7) Translating functions

8) Transforming functions

9) Solving equations and inequalities graphically

Update:
Quiz 3 scores:
10| 0 0
9| 2 6 8 8 8
8| 0 2 6
7| 6 6 8
6| 0 4 4 6 8 8
5| 0 4
4|
3| 2
2|
1|

The class seems to have split into those that really understood and those who didn't. There's something about inequality signs that just drives some kids bonkers.

Critical Thinking

I have this Escher drawing on the desktop of my laptop. When showing grades to students, one noticed the picture and said, "Is that your house?".

Next Lesson: Solving Equations and Inequalities Graphically

This is the final lesson of the unit, aside from review and the test. The objective is for students to apply their understanding of graphical representations to be able to solve inequalities and equations.

After reviewing the homework, students will work on a Do Now worksheet with a graph of a parabola and some dotted horizontal and vertical lines. They are asked to use the graph and the lines to solve equations and inequalities.

Following this, there will be some direct instruction on solving graphically. The idea I want to present is:

To solve an equation or inequality graphically:
a) Write each side of the equation/inequality as a function
b) Graph the functions
c) Find the intersection point(s) (and draw dotted vertical “helper” lines)
d) Determine the part of the domain that solves the initial problem

We will review the absolute value problems they solved in the first unit (i.e. |x + 3| > 4), solving them graphically. I will also show them how to find points of intersection on the TI-83+. We will compare solving these graphically to solving them algebraically. Hopefully, students will see that a "less than" inequality makes a "sandwich" graph on the number line because the tip of the V is dipping below the horizontal line (does that make sense?). A "greater than" inequality makes a "gap" graph on the number line because the tops of the V go above the horizontal line to the left and right of the points of intersection.

After direct instruction, students will work independently to practice these concepts. The homework includes solving quadratic equations/inequalities in the same way. Students will also review for the third quiz (on this, plus translation and transformation of functions).

Aggressive Problem Solving

Question: "What shape will the graph of y = |mx + b| always make?"
Answer: "It'll make a fucken V shape."

I suggested to the student that, on future quizzes, he pick a different adjective to describe his graphs.

I don't know where this came from - in all my years, I've never gotten a response like that. At least he was correct, though he needs to work on his spelling.

How much is a million?

It's been a long time since I posted about the Numeracy class, mainly because I am not teaching it this year, so it's no longer at the front of my mind. But, this year's Numeracy teachers are struggling with the same concepts that I did. One of these killer concepts is rounding. This does not seem like a very difficult idea, but for our students, learning how to round a number is a huge challenge. We've tried all sorts of scaffolding, conceptual development, practice with the algorithm, and some kids just can't get it.

Ultimately, we think it comes down to a continued lack of understanding of the base-10 system. These students missed out on some very important mathematics in their first few years of school, and this is making everything else inordinately difficult for them. This week, one of the classes is piloting an activity where the students have the goal of collecting one million pennies. Each day, students will have to count how many pennies there are so far (pennies will initially be collected in a big jar). The idea is that students will eventually lose patience with this, and propose the idea of some sort of stacking or grouping. The teacher will then magically produce a container that has slots to divide the pennies into groups! When groups of 10 are no longer enough, then bigger groups of 100 will be used, and so forth.

Aside from learning more about the base-10 system, and the relative sizes of the different places, we hope that this activity will help students understand more about large numbers. We do an activity in the class where the whiteboard is divided into categories (thousands, millions, billions, trillions), and teams are given strips of paper with a quantity and a number, anad they must stick it to the board in the right column. For example, a strip might read "Number of people in San Jose (1)", or "The average income of a family of four (50)". It should come as no surprise that students usually have no idea where to put the strips of paper. In any case, this year's students seem to really doubt that there are about a million people in San Jose - they think the number is bigger by orders of magnitude. With the pennies activity, students will hopefully see that reaching a million is a bit harder than they think. But if they do reach a million, they will definitely earn their pizza party!

Next Lesson: Transforming Functions

My renewed enthusiasm for old childhood joys has come at an opportune time. In Tuesday's lesson, we will be working on transforming functions. I have a few transformers that have (incredibly) survived until now, which are currently gathering dust on my mantle. Hmm... do I bring in the opportunistic, irritating Starscream, the powerful, pea-brained Grimlock, or, everyone's favorite transforming boombox, Soundwave (though his head is broken off and I don't have any of his tape-minions).

In any case, my idea for this lesson is to have the students work on a scaffolded exploration for most of the class. They will work on learning transformations, as well as absolute value (of linear) functions. They can work individually, in pairs, or in groups, but each person must turn in their own paper by the end, and it will be graded like a quiz. The exploration/quiz is broken into 4 parts:

1) Creating absolute value functions.
In this part, students will graph a linear function. They will then graph the absolute value of the same line by looking at the y-coordinates of several points, and plotting their absolute values. They will have to then answer questions that help them see that y = |mx + b| will always make a V shape.

2) Translating absolute value functions.
In this part, students will review horizontal and vertical shifts from the previous lesson, but applied to absolute value functions.

3) Transforming absolute value functions.
In this part, students will plot out y = |x| and various transformations in the form y = a|x| to see what happens. By the end of this part, they should have a good sense for how the coefficient a affects the shape of the graph.

4) Synthesis
In the final part, students will put together what they know about translations and transformations to create the graph of f(x) = 2|x + 4| - 3. Then, they will generate a table and see if their ordered pairs fall on the graph that was created via the translation/transformation process.

After this, we will end the class with 15 - 20 minutes of direct instruction where I help formalize their understanding of transformations. I'm worried about running out of time for this. If I do, I can push it to the next class, and that will be ok, though it would be better in the same period. I hope that making the exploration into a quiz will help students focus and be more efficient with their time.

The lesson will be posted on ILoveMath.

Update:
Whoops.. I forgot that the entire sophomore class is out on a field trip to the Monterey Bay Aquarium for biology. My classes today have had about 4 people each. I got some good one-on-one time with my handful of juniors, and I'll just have to push things back to Thursday.

80's Cartoons Say it Best!

"Leadership, my sine function" - Starscream

(said derisively of Megatron's prowess as a commander)

Next Lesson: Translating Functions

Tomorrow, we will be leaving piecewise functions behind for a while. The students this year are doing better overall than last year, but some students still are having significant struggles with understanding piecewise functions. When asked to graph a single line in a restricted domain, that seems to be fine. But as soon as the pieces are put together, students get very confused between the f(x) value from the equation, and the x-values from the domain condition (I haven't graded the quiz yet, so I'll have some better information about this soon).

We'll come back to it when we review for the unit test and the final exam, but for now, we need to move on. The goal for the next lesson is for students to understand vertical and horizontal shifts - why they happen, how to determine the shift, and how to generate translated graphs.

For the Do Now, students will be asked to plot out y = x^2 and y = x^2 + 3, and compare the graphs. They will do the same for y = x^2 and y = (x - 2)^2. At this point, they are working by hand so that they can, point by point, see what is happening. We will discuss their results and get some initial conjectures out. Then, they will do a graphing calculator exploration of the same ideas, which will allow them to graph more functions more quickly.

After this, we'll put the ideas together as I do some direct instruction, and define the concepts of vertical and horizontal shift. We will use what they've learned to understand why the vertex of y = a(x - h)^2 + k is (h, k) - which is, after all, a state standard! Yes! I hope that providing more scaffolding on translations will help them understand the vertex form better. I also think it will help them be more prepared for all those crazy phase-shifting, period changing trig functions they will encounter in pre-calc (along with the upcoming lesson, which will look at stretching transformations, in general and with specific attention to absolute value functions).

Update:
I graded quiz 2 and the scores were lower than I'd hoped:
10| 0
9| 0 3 3
8| 0 3 3 3 5 8 8
7| 1 3 3 6 6 8
6| 3 6 8
5| 1 4 6
4| 4
3|
2| 0
1|

There were too many students who crashed on this one, although the bulk of the class was still in a good range. Many students had trouble with inequality notation - after working so heavily on interval notation, they seem to have forgotten how to use inequality notation, which is something they were already familiar with. For example, to express the numbers less than 3, we write (-infinity, 3) . Several students then wrote something like -infinity < x < 3 instead of just x < 3. It is always very interesting to me how new knowledge seems to crowd out old knowledge for a while, and then there is a process of assimilation where the mind brings them together and eventually sorts it out. The piecewise question was decent overall, although there are quite a few students who have not mastered it yet. I think that it needs some time to marinate in their brains, and we'll review these problems when we get toward the unit test. I think I'll develop a good error-checking handout for them to work on.

Next Lesson: Determining the function of a piecewise graph and Quiz 2

In the next class, we will start by reviewing the homework in a different manner than normal. We'll do the more traditional "I'll put the answers on the overhead, and we will go through it together to see if there are any questions" instead of my new homework review process . This is because the homework is long and has lots of short questions, and it is the review sheet for the day's quiz. I hope that reviewing the work this way today will be effective.

After the review, we will have a team challenge that is worth points on the quiz - not extra credit, but the normal, quotidian kind - 9 out of the 50 points. Teams will be given three 3-point problems, one at a time. They can work in their teams, use notes, and ask me a total of 3 questions for the whole activity. When they agree to a solution, they all sign off on that sheet and turn it in to me, getting the next problem in return. If anyone talks to a different team, they will lose 1 point from their score. I think that these rules will help keep them focused on their work and helping their teammates.

Problem 1: Given a piecewise function, make a graph

Problem 2: Given a graph of a piecewise function, determine the equations. (My hope is that they can work this out on their own, though they haven't gone in the backwards direction yet. They can use one of their 3 questions here, of course)

Problem 3: Given a graph of two lines that are not crossing, but clearly will cross, determine the exact point of intersection. (To do this, they have to determine the function of each line, and then solve the system algebraically. I think there will be a lot of confusion here, but if they ask me a good question, they should be able to proceed).

I haven't tried something like this before, so we'll see how it goes.

We'll then take a few minutes where I show them the answers and deal with any last minute questions. The class will then have the last 30 minutes to take the quiz.

The homework will focus on determining the functions of given piecewise graphs, along with review of solving absolute value inequalities and equations in preparation for the upcoming lessons in which we will solve these same problems graphically.

Next Lesson: More Piecewise Functions

This lesson will start out with students warming up on a piecewise function with only linear parts, as in the homework. The graph is followed by a series of evaluation problems. The first can be done by looking at the graph - the rest require use of the equations. This will be explained later in the class; for now, the idea is to see if students can figure out how to do it, either alone or by working together.

After reviewing this, we will add to the notes from the previous lesson. I'll show the students how to evaluate a piecewise function algebraically by determining which condition is made true by the x-value, and then substituting the x-value into the corresponding equation. We can use this idea to go back to the Do Now problems if they didn't figure them out. I will set up an x-y table to record the values we test during this portion of the lesson - next, we'll use tables to graph more complicated functions.

At this point, I'll hand out a reading to the students that shows how to use a table to help graph a piecewise function that has non-linear pieces (like absolute values, quadratics, etc.). My idea is that they will write the x-values that are the endpoints of the conditions twice in the table, and evaluate them with each of the equation parts. They will indicate on the table if the y-value is a closed or open circle. Students will then have time to practice this independently.

Homework is a set of problems that will help them review for the second quiz in the next class.

Next Lesson: Graphing Piecewise Functions

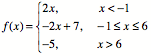
Graphing a piecewise function is one of those topics which initially doesn't seem that challenging, but I've found that students get very confused. They tend to flip back and forth between x and f(x) in their minds, and their graphs often come out totally funky. Last year, I had to backtrack and re-scaffold my lessons when I saw how tough it was. This year, I think I have a better plan.

In this lesson, after reviewing homework and warming up with more graphical analysis (see previous post), students will do more practice graphing a simple slope-intercept linear function in a restricted domain. They will do these one at a time, so they can focus on the relationship between the graph (i.e. the y-values) and the interval they are graphing on (i.e. the x-values).

Once they've got that down, I'll do some direct instruction where I show them what a piecewise function looks like, and how it can be thought of as simply putting together the restricted domain lines they were just doing into one graph. Today, we will only look at piecewise functions whose parts are constant or linear. We will go through one example together as a class, and then they will try to do one on their own.

The homework will ask them to graph two more piecewise functions, and then to do another graphical analysis problem. On that problem, they are given two linear functions f(x) and g(x), and asked to find things like f(2) * g(2) and g(4) / f(4). This is early preparation for the quadratic and rational functions units, where I ask students to graph a pair of linear functions and then point-by-point multiply (parabola) or divide (hyperbola) the y-values to create the new function. As a bonus on this homework, I am asking them to make a graph of |f(x)| and |g(x)| to see if they can connect what they know about absolute value and graphical representations to generate the v-shaped graph on their own.

Next Lesson: Domain and Range

Tomorrow, we'll start class by reviewing the homework (as always), and then I get to give students back their quiz and congratulate them on doing so well. That's always more fun for everyone than when they do poorly.

Next, students will work individually on more graphical analysis work, as in the last lesson. I'm convinced that fluidity with graphical representation is a key skill that must be continually reinforced. When I first started at DCP, I taught primarily Algebra 1. I never understood why students could graph a system of equations and find the intersection point, solve a system algebraically, but not make the connection between the point of intersection and the algebraic solution. It took me a while to see that they did not really understand the relationship between "y = 2x + 3" and the graph that they knew how to produce. Without that understanding, it becomes clear why a point of intersection seems to have nothing to do with algebra.

Anyway, following this, there will be some direct instruction where I show students a series of graphs, and help them understand how to determine the domain and range, and write them in interval and inequality notation.

Finally, there will be time for pair work practice where students will determine the domain and range of given graphs. They will also have to graph a linear function over a restricted domain. Understanding how to do this will make the upcoming piecewise functions lesson much more successful.

The homework will be practice of these concepts, with some review problems thrown in. I've been thinking about including function decomposition in the curriculum - I decided to put in some problems on this homework (shown above) where they must match a composite function with a pair of component functions as a sort of first step in that direction. We'll see how they do with it.

Update:
I've compiled six graphs with related questions that push on students' understanding of how a graph represents a function. I've uploaded them to ILoveMath in the Algebra: Misc Topics section. If you use any of my stuff, I'd love to get any feedback.

Next Lesson: Function Operations

Ok, this was actually last Friday's lesson..

We had the first quiz of the second unit. Students did well - the average score was a 79%. After this, we began exploring graphical analysis. The example shown here is part of the homework. As predicted, answering these types of questions was hard for many of the students, but we did seem to make some good progress. I didn't give them any direct instruction - just asked them to try to figure out the questions in their groups based on what they already know. Then, we reviewed the answers together. We will keep coming back to these types of problems in the upcoming lessons.

After this, I did direct instruction on adding, subtracting, and multiplying functions. Students liked this, because it only required use of their algebra 1 skills. Though the notation was different, they didn't have to learn anything "new"; the feeling of relief was almost palpable in the room.

Standards Coverage

In a comment in the previous post, Darren says:

I find the Algebra 2 standards to be fairly "aggressive", like drinking water from a fire hose. How you find time to add in topics that are not in the standards, I don't know but would be most interested in learning.

(I think it is worth starting a new post to answer this... I'm interested, as always, to hear people's thoughts.)

Well, you're right. We are not able to adequately cover all the standards as they are written, especially since our students start so far behind the curve. What we've done is to strand out the standards over the 4 years. We leave some things out of Algebra 1, and push them into Algebra 2. Some of the Algebra 2 standards we then move into Pre-Calc. And some, we decide not to do at all.

When deciding what to cover (and in what depth) in Algebra 2 Honors, I look not just at the list of state standards, but at the blueprint for the standardized test (i.e. what are the key standards that comprise the bulk of the test), at what will be covered in Geometry and Pre-Calc, and at what will be most useful for students moving in a trajectory toward Calculus.

I know we can't do it all, so my goal is to balance the required coverage with a strong scaffolding for success in Calculus - all with an eye to who our target student is.

For example, though I think conic sections is a great topic, a thorough unit would take my students many lessons to master - yet there is only one single question on the test. So we leave it for Pre-Calc.

The same is true for combinations, permutations, probability and stats, mathematical induction, series - all together these topics comprise just about 20% of the test. I choose to focus on the rest, and go deeper by including relevant scaffolding, math analysis components, word problems, and so forth.

With our students, I believe this actually yields higher test scores than covering everything more shallowly would.

Update:
There is discussion of this going on at Darren's site if you are interested.

Next Lesson: Representational Fluency

The composition lesson went fairly well, though I could have used about 5 more minutes to finish the lecture. Students seemed comfortable with finding things like f(g(2)), but I definitely lost many of them when I tried to finish with finding f(g(x)) as an expression. We'll definitely need to review this a couple of times.

In the next lesson, after reviewing the homework, the Do Now will focus on practicing these concepts (as well as reviewing absolute value inequalities).

Then, I'm going to squeeze in a mini-lesson on using the TI-83+ to graph inequalities and absolute value inequalities. In this case, I mean graphing things like y = (x < 5), where it returns 1 if true and 0 if false. This is a pretty cool way to generate a graph that looks like the number lines we shade by hand. It can solve absolute value problems the same way: y = (abs(2x+1) > 3). After learning this technique, students will check their answers from the Do Now by graphing. I'm hoping that this doesn't take too much time...

Finally, I will give students a handout on Representational Fluency. I've learned from my experiences teaching AP Calculus in previous years how important it is for students to be able to move comfortably between equations, graphs, tables, verbal descriptions, arrow mappings, etc - especially when it comes to the concept of functions. This sheet focuses on graph and table representations of functions - students have to figure out things like f(2) and f(g(-2)) from these representations. I'll post this on ILoveMath .

Update:
I'm trying to decide if I should do some work on function decomposition. This is clearly a skill that students will need for Calculus (i.e. working with the chain rule). I also think that decomposing functions might help them understand better what composing functions really means. But I'm also worried about overloading them, and I wonder if they need more time to digest function notation and composition first. It's not in the standards, as far as I can tell, so I wonder if students are expected to understand this idea before getting to Calculus. Any ideas?

Next Lesson: Function Composition

Up next, students will learn to evaluate composite functions. First, they will do a worksheet with function notation practice problems. I set the problems up in groups of 4 as follows: f(2), f(-4), f(a), f(2x - 5). I think that sneaking up this way on the idea of plugging in an expression for x will help students better understand how to evaluate f(g(x)) as an expression. I remember having a lot of difficulty when I first learned this concept, and this method helps make it clearer for me anyway...

Then, we'll use this dual lens model. I hope it will help them visualize what "the output of f is the input of g" means. After the model, we'll go through the concept of composing functions, and do some example problems together.

In an upcoming class, I will give students a chance to do function composition when given graphs or tables instead of equations.

Next Lesson: Functions and Relations

Today's lesson was simply a chance for the students to begin working with their graphing calculators. I have a bunch of squirrely boys in the class, and they take to the TI-83+ like it was a Game Boy. It's amazing - I can show one of them how to do something once, and 5 minutes later half the class will be experts in it. I can give the same students directions about organizing their binders five times, verbally and in print, and there will still be tons of questions. It just goes to show how important motivation is in the learning process. One of my students keeps asking me where to find the games - after all, that's the whole point of getting one of these things!

Tomorrow, we begin the second unit, which focuses on functions. It's not going to be the most exciting lesson, as it will be primarily direct instruction.

The class starts with an introduction to functions, with the metaphor of a lens. I have two vertical number lines on a handout, with a picture of a lens (which I made in Google Sketchup) in the middle. The directions ask them to draw a stick figure on the left (the original image), with the feet at 0, the knees at 1, the hips at 2, the shoulders at 3, and the top of the head at 4. The lens is a "y = x^2" function, and they must map the projection onto the second number line by drawing guiding arrows from the inputs to the matching outputs. Later, when we do composition, I will use a double lens model to show how the projected image can then be used as the input of the second lens.

After that, we'll look at the definition of relations and functions, and I'll present them with functions in various forms: tables, arrow mappings, equations, graphs, and sets of ordered pairs. It's all about multirepresentational fluency, baby! We'll end that section with the vertical line test, and then learn about function notation.

I realized I screwed up on the homework I assigned from today's calculator lesson - I asked them to sketch a graph of f(x) = cos x. In my tutorial, I saw kids typing into their TIs: Y1 = F(x)cos(x). I forgot that I hadn't taught them yet what f(x) means. I'll just say what the freshmen say when they make a mistake: "just kidding!"

Unit 1 results are in!

I'm happy and relieved to say that our first test went pretty well. It was the right length - all students finished, but needed to work most of the period. I gave them a 7 page test (it was single-sided, and the last page was extra credit problems), and it was guiltily satisfying to hear their gasps of fear when I dropped them on the table in front of them.

I graded them quickly, because I was so anxious, and the results were nice:
Mean = 76%
Median = 79%

Here is a stem-leaf plot of the scores:

10| 0 3
9| 0 1 2 3 8
8| 0 1 2 4 8 9
7| 1 1 3 5 8
6| 1 2 4
5| 0 9 9
4| 8
3| 7
2|
1|


There was no single section that students missed across the board. I found lots of little mistakes that were common, and so I need to make sure to work those in as we move forward. I am trying to make more of an effort this year to constantly spiral in previous topics so they don't get lost.

Breakfast of Champions

Apparently, I found my new shirt to be a lot funnier than the students did...

Next Lesson: Study Groups

Ok, it's actually the last lesson I did, but I didn't have any time to post, what with Back to School Night and other stuff going on this week.

Tuesday is the first unit test for my Algebra 2 class. The first unit test is when reality sinks in for everyone... and we'll see if any of the students decide that they want to switch out of the honors class. I think a few might, but most of them - even if they are struggling - are really showing a lot of determination, which is impressive. I even have a few students who were in Numeracy last year as freshmen (meaning that they came to high school with math skills below a 7th grade level), and now they are in my honors class. I try not to play favorites, but I just have such a soft spot for them. Last year I was helping them learn how to add and multiply fractions, and by the end of this year they will be graphing complicated rational functions and solving 3 x 3 systems of equations. Now that's what you call ganas!

Anyway, one of the skills I want my students to learn is how to effectively use a study group to prepare for a test. Like everything else, this does not come naturally to them, and it needs to be scaffolded. So, after the normal homework review and Do Now practice problems, we did the following:

1) I gave them a handout detailing how they should organize their binders. They have a table of contents at the front, in which they enter each lesson's topic. Each of these entries corresponds to a page of notes, which should be in order at the beginning of the tab (each unit has its own tab). Following the notes, they keep all important handouts relating to the unit, and then all of their homework assignments (each assignment should have the original worksheet, their solutions, and any corrections all staples together). At the end of each unit, I ask them to go through the handouts and recycle (or at least remove from the binder) anything that they probably won't go back to and use anymore. I am trying to get them to learn how to evaluate the importance of materials (i.e. "hmm, this page of important looking notes I should probably keep, while this 10-minute in class worksheet we did can probably go...").

2) I gave them another handout with a structure for how to work in a study group. Here's the text:

How to Study in Groups for a Math Test!

1) Identify the sections that are on the test.
a. From a review sheet
b. From your notes, quizzes, and homeworks

2) Locate sample problems for each section.
a. From old quizzes/tests
b. From notes
c. From homework
(in that order!)

3) Figure out which sections are most difficult for you as an individual.

4) Figure out which sections you want to start on as a group.

5) Begin working on individual problems. Use a clean sheet of binder paper to do this – don’t write on top of your old problem. There are several ways you can structure this.
a. Each person works on the same problem first, and then everyone compares answers.
b. One person who knows how to do a problem shows the rest of the group.
c. Each person in the group works at their own pace, and asks for help as needed.

6) When you are stuck, do the following things in order:
a. Check your notes.
b. Ask someone in your group.
c. Ask your friendly teacher.

3) Then, because this was their first time, I gave them the sections that would be on the test (i.e. step 1). I told them that by the third or fourth unit test, I would expect them to be able to do this part on their own. I asked them to rank each section (0 = I don't remember this at all; 1 = I need someone to help me on this; 2 = I just need to practice this by myself; 3 = I am ready to do this on the test), and then to discuss their ranks as a group and come up with a plan of attack.

4) After that, groups had about 30 minutes left to begin their studying. This does feel like a lot of time to use up on not actually reviewing problems - I think it will have a long term benefit if I stick with it, but I might have to be prepared for some short term hits. Most of the groups took it seriously and they all had different styles to how they worked on the problems, and what problems they chose to focus on.

5) For homework, I gave them their practice test problems. I decided to not let them have it until the end of class, because they would have just done those problems and avoided looking through their old quizzes and notes.

So that's that. Wish them luck! I'll post the outcome of the test next week sometime. In case you're interested, and still reading, here are the topics that are on this test. (It's kind of a hodgepodge of review and new topics... I haven't figured out a way to do this unit better yet. I can't wait to get into unit 2, because it is all new and it has a more consistent structure.)

Unit 1 Test Sections
1) The real number system (types of numbers and properties of real numbers)

2) Solving equations with rational coefficients (fractions and decimals in front of the variables)

3) Converting decimals to fractions (including repeating decimals like 0.4222...)

4) Working with parallel and perpendicular lines

5) Systems of equations (linear combination, word problems)

6) Isolating a variable (even complicated ones, and when the variable is in the denominator)

7) Solving and graphing compound inequalities (AND and OR inequalities)

8) Using interval notation (going between number lines, inequalities, and interval notation)

9) Absolute value equations

10) Absolute value inequalities

Next Lesson: Absolute Value Inequalities

The last lesson seemed to go fine. Half of the class time was devoted to doing our computerized math grade level diagnostic testing, so I didn't really get a chance to see if they mastered the objective. I'll have to see how their homework comes in.

In tomorrow's lesson, we will begin with an error-checking Do Now. Students are given a series of problems (in this case, mainly focused on converting between number lines, interval notation, and inequality notation) that are already worked out, and must determine whether or not they are correct. If the problems are incorrect, students must identify, explain, and correct the error. I'm trying to do these kinds of activities more frequently, to build students abilities to reflect on mathematical solutions and identify common sources of error.

After this, we will extend the 5-step model used for solving absolute value equations to inequalities. Everything is basically the same - the hardest parts for students tends to be drawing a number line that represents the inequality, and then converting that number line into a compound inequality. I'm predicting that the work done in the Do Now will be sufficient scaffolding for this to be less of a challenge (I've definitely learned from mistakes made last year!).

The class will then have about 20 - 25 minutes to practice these problems individually or in pairs. I really hope I don't cut in to this time too much. For my students, this type of practice time in class, immediately following direct instruction, seems to be indispensable. But it is all to easy to go on and on during direct instruction, trying to get every last one of the students to understand what you're saying. This is never going to happen, obviously, but there is something that seems to compel me when I'm in front of the class to keep going, answer every single question, and make sure every student is ready to work. I've been working with a timer this year for the first time, and that seems to help. I do tend to say things to the timer when it gives me a warning beep ("alright, alright, I'm hurrying!") and the students look at me funny.

Anyway, handouts to be posted on ILoveMath.org.

Next Lesson: Absolute Value Equations

For Tuesday's lesson, we will be looking at the meaning of absolute value, and how to solve absolute value equations. I decided to go with the traditional idea of treating |x| as the distance between x and 0, and using that as the base for solving equations such as 2|x - 5| - 8 = 4. The method we will use is:
1) isolate the absolute value
2) write the meaning in words (just for now, until it sinks in)
3) draw a number line
4) use the number line to write 2 equations and solve them
5) plot the final solutions on a new number line

This is different than what we are doing in the regular (not honors) algebra 2 classes. There, the method is pretty much the same, but we are teaching them the fundamental concept that |x - a| is the distance between x and a. They are being taught to rewrite any absolute value equation in that form first. I think it is helping them solve the basic equations and inequalities, and it is definitely helping them with the "tolerance" word problems. That's ok for the regular class, because that satisfies the standards for absolute value, and they won't be doing anything else with it for the rest of the year.

My impression, though, is that teaching it this way somehow would make it harder if you go on to study absolute value functions. For example, I want my honors students, if given a graphical representation of a function (and not necessarily the equation), to be able to graph the absolute value of that function. I think that this requires you to think of the absolute value as something that always returns a positive value (i.e. the magnitude of the distance from 0), and not necessarily the distance between two non-zero numbers. I really believe that this type of representational fluency is necessary for them to be able to understand Calculus. Anyway, if anyone has any reactions or advice, please feel free to leave a comment.

The handout and sample problems I will use for this lesson can be found on ILoveMath.

Slam I Am

I really enjoy teaching math. I like working on math problems myself, and I find reading about the history of mathematics to be fascinating, but I'm no mathematician. When I first got interested in education, I definitely saw myself as more of a humanities person - probably English. It was actually subbing at DCP (before I taught there full time) that convinced me to become a math teacher instead. Our freshmen come in knowing very little about anything academic, to be quite honest, and watching them struggle through writing a simple sentence, I knew that English class (at least for the first 2 or 3 years) would not be about reading great books and having deep class discussion. Their math abilities were in comparable disarray, but it seemed like a more manageable problem - teaching math is much more linear than English. I've since learned that, even when students struggle with basic oral and written communication, it's still possible for the classes and assignments to be quite interesting. I like pushing the students on their numeracy, problem solving, and critical thinking skills, but I definitely miss being able to connect with students on a different level - i.e. hearing their thoughts about life, reading what they write about their families and friends, and so forth. I'm too busy pushing them to the next math standard.

Last year, through a partnership with MACLA, a local Latin American arts and culture venue (if you live in South Bay, I highly recommend you click the link and check it out!), another teacher and I began the DCP Slam Poetry team. MACLA hosts the South Bay Teen Slam League, and they offer free Friday poetry workshops to high school students. We had a few students last year who were regulars, and even competed in one or two slams, but we never had enough momentum to really get off the ground. Yesterday, we began the new season, and we took over about 15 students. The room was packed and the students really had a good time. It's an uncensored workshop and it's hosted by local poets (not musty old teachers). Though the actual "teaching of poetry" part of the workshop is not always the strongest, it gives the students a great venue for saying whatever the hell they want to say. I bring the students there, and I usually stay and listen to what goes on (brainstorms and free-writes, improv activities, read-alouds, etc.), but I don't participate at all. They get into it, and soon I'm not there - they begin to talk like they do outside of school. I like being able to not monitor what they are saying and to just listen. My goal this year is to actually engage in the same writing activities that they do (they always asked me why I wasn't writing, and what could I say?). So we'll see.. if I actually end up writing a good poem maybe I'll post it. I hope that enough students stay interested in it, and that the team will have enough momentum to move forward on its own. It's an amazing thing to see how empowering it is to those who muster the courage to get up on stage and (for lack of a less cliche description) bare their souls. When they finally perform, they come off the stage crackling with energy and life (which is not necessarily the normal state of being for a teenager!)

Next Lesson: Compound Inequalities and Interval Notation

After reviewing the homework and the results of the last quiz (mean: 76%, not great, not terrible), we will dive in to a little guided instruction time.

We'll start with a quick review of inequalities - students will add, subtract, multiply, and divide the inequality 4 < 8 by both 2 and -2 to see which operations cause the inequality symbol to reverse. We'll also review the idea that a < b means that a exists to the left of b - some students have problems with this, especially when the numbers are negative. We'll also see why x < a is the same as a > x, and that when graphing, you can't just draw an arrow in the direction that the inequality symbol faces.

Then, I'll show them how to solve and graph both simple and compound inequalities. I'll do a couple of examples, and then they will also.

Finally, I'll hand out a reading that introduces students to interval notation. They will read it and then complete the practice problems on their own, as I walk around and coach them. This topic is not part of the standards, but it is used extensively in Calculus, and I think Algebra 2 is the right place for students to see it. The handout (with problems) is on ILoveMath.org.

Update:
The lesson went fine, but there was not enough time for the students to complete the interval notation reading, so I'm pushing that to the next class. They were asking good questions about inequalities (i.e. why expressions like 3 < x > 6, or -2 > x > 2 don't make sense). These students seem to have retained a lot from Algebra 1, which is always a good sign!

Next Lesson: Isolating a Variable

In this lesson, students will learn how to solve for a variable that may be in multiple terms, as well as trapped inside of parentheses. I realized I needed to make this a specific objective in Algebra 2 when my Calculus students in previous years didn't know how to isolate dy/dx after taking an implicit derivative. They have also had trouble in science: for example, the Gas Laws in Chemistry throw them for a loop when they have to solve for a variable that's in the denominator. Hopefully, getting in some good practice with this solving technique now will pay off when it is reinforced later on.

We will start by looking at x + xy = 1, and finding the value of y for different values of x. Students will likely conclude that it would be easier to isolate y first. We'll then look at some specific formulas (Gas Laws, temperature conversion) and how to isolate for any given variable. The key to isolating a variable:
1) use the distributive property (if the variable is trapped inside parentheses).
2) get all the terms with the variable on one side of the equation.
3) get all the terms without the variable on the other side.
4) if necessary, factor the variable out, and then divide what remains.

The type of problem I want them to be able to do: Isolate y in (3 + 7x)y – 6(xy + 5) = 15

Following the direct instruction portion, students will have independent practice time with a related homework. These will be posted on ILoveMath.

Update:
The lesson went ok, but I realized I made the same mistake as last year... I need to teach students how to deal with the division form of the distributive property first, so they can understand why certain steps are invalid. For example, given the equation xy = 2y + 7, students will tend to "divide both sides by y" to get x = 2 + 7. I didn't think of this because none of the problems I gave require a division step like that - but I forgot to take into account that they would mistakenly do it. Woops. I think that will come up in the next lesson.

Next Lesson: 2 x 2 systems practice

The students liked learning the linear combination method. I like to play up things like that for them - "Now that you're in Algebra 2, you're ready to learn this new technique..." Of course, I screwed up my first example, which was supposed to have a simple integer solution - I copied the wrong number down in the problem and we ended with thirteenths or something, and then I decided to push ahead anyways (cause everyone loves fraction practice!).. So after thoroughly losing them, I started over with the other examples, and they caught on pretty quickly.

Next class:
- Students will practice solving linear equations with rational coefficients. I am using the "partner problems" idea that I saw on ILoveMath.org - you put the problems in two columns, where the matching problems are different but have the same answer. This way, students work on their own problem, but can easily check if they are getting it right by comparing their results to their partner.

- Then, I will do a brief direct instruction piece where we work through solving a 2 x 2 system word problem together following the key steps (identify the variables, write the equations, solve, answer in a sentence) on the overhead.

- Finally, students will practice with more word problems in the Problem Relay format. Each group selects a runner. I sit at the front with a stack of problems for each group. The runners get the first problem and the teams work. They send the runner up when they are finished to have the problems checked. If they are right, they move on to the next problem. If they are wrong, they get a penalty (either points or time lost) - and I use my own discretion to determine what kind of help to give them. At the end, the team with the most correctly solved problems will earn some mythical extra homework points.

Update:
The students loved the relay game. Almost everyone was working full-tilt for 30 minutes straight. One of my students has Asperger's and he was chosen to be a problem runner for his team. He took it a little too seriously - the first time his team finished a problem, he launched himself at me full speed, and I literally had to fend him off so that he didn't crash into me. I coached him a little on how to properly bring the problem up; the next time, he ran the same way, but stopped himself in time, and only knocked a bunch of papers off the table. He's a funny kid - the only student at our school who is on a "no reading" contract, and who gets his books taken away (like others lose their cell phones) because he won't ever stop reading, even in class. Anyway, we'll have to do this activity again in a few weeks.