
Kate wrote a great post about the value of a well-structured worksheet last month.
I agree that there are huge benefits of having a unified task, with some type of self-checking or affirmation. And a little fun and/or creativity doesn't hurt. Joke worksheets do that pretty well. However, my students (who are generally not native English speakers) hardly ever get the joke. They tackle the sheet with excitement, but there is usually that little moment of disappointment at the end when they don't get the punchline. Instead, of course, of the expected groan and eye-roll that accompanies a quality pun.
"What do you get when you mix prune juice with holy water?"
"A religious movement"
After two minutes of explanation, that loses some of its original zing.
So my question is if anyone has or knows about these kinds of worksheets developed for ELL students? I'm kind of doubting that there are any, but it never hurts to ask. I think I will probably end up creating some next semester, with jokes solicited from my students. Then I can publish the DCP Spanglish Algebra Joke Book.
Thursday, December 17, 2009
ELL Joke Worksheets?
Posted by
Dan Wekselgreene
7
comments
![]()
Tuesday, December 15, 2009
Algebra 1: Situation Graphing

I learned a few years back that jumping right into graphing slope-intercept equations never worked. This is one of those concepts that, before I became a math teacher, I never would have guessed would be so hard for students to master. Start at the y-intercept, use the rate of change to plot the next point, and you're done - right? Yeah, not really. So after a couple of years of teaching, reteaching, re-reteaching, and tearing my hair out, I decided to try some other things. Eventually, I realized that a ton of scaffolding of the concept of slope was needed, along with firmly rooting linear functions in situated contexts.
One of the constant problem areas is deciding which way to draw the line for a negative slope. To graph something like y = -(2/3)x + 5, students would often move down 2 and left 3. My old attempts at correcting this focused only on the mathematical explanation: -(2/3) = -2/3 = 2/-3. So, you either go down 2 and right 3, or up 2 and left 3. If you go down 2 and left 3, that means -2/-3, which is 2/3. This is a perfectly reasonable way to explain it, but it didn't really provide much of a lifeline to my lower-skilled students, as it hinges on mastery of the division rules of signs, as well as remembering that a fraction also represents a division problem.
The other common problem was for students to correctly identify the starting point number, but to plot it on the x-axis instead of the y-axis.
The way I run the unit now is to provide numerous opportunities to graph and describe situations, both with and without numbers, in just the first quadrant of the coordinate plane. Distance, income, height, and so on. The quantity being measured is always on the vertical axis, and the horizontal axis always represents time. When we eventually generalize to y = mx + b equations on the full coordinate plane, I use the situated contexts as memory anchors. If a student doesn't remember where to start, I say something like, "Where do we show that the Hare got a two foot head start? On the feet axis or on the seconds axis?" In these situations, a positive rate of change always means "moving up" and a negative rate of change always means "moving down", while time is always passing to the right. This is a much more helpful way for my students to think about how to graph their decontextualized lines. Suddenly, there is a reason for the direction the line is moving in, instead of just a sign rule.
Another benefit to this approach is that my students are now a lot more flexible with the form of the equations. My situated equations typically are in the form y = b + mx, which seems like a more natural connection to the preferred method for graphing. Once they grasp that the number without the variable is always the starting point, then they can handle both y = b + mx and y = mx + b relatively interchangeably. Also, it really helps them to understand the difference between equations like y = 2 and y = 2x. The first shows a starting point of 2, with zero rate of change. What does it look like on a graph if someone is not moving, but time is still passing? Exactly - a straight line! (I'm still working on that one - even my highest skilled students still say straight when they mean horizontal. My "all lines are straight" response doesn't usually clarify the way I'd like it to.) And in the second, the rate of change is 2. Ahh, it's like a graph of someone running 2 feet per second... but where did he start from? Zero? Where is that?
This approach takes a ton more time, of course, but I can't see any way around it for my students. I hope that I am providing them with a long-lasting ability to understand and graph linear functions. The semester is ending this week (final exams start tomorrow!), so the test will be to see how much they recall in January, when we move into the next unit. We'll be doing those oh-so-fun problems where you give them a point and a slope (or a parallel line and a point, or two points) and they have to give you the equation of the line. I'm going to experiment with doing every problem both graphically and algebraically (both in instruction and on assessments) to see if the focus on multiple representations helps them master these problems. I'll post more about that in late January (after I develop and teach it!).
My Slope and Graphing Linear Functions unit (Unit 4) is pretty much up-to-date in my box.com widget in the side bar. Here are a couple of examples (in pdf format) of the kinds of activities that they were doing. The Word and Keynote files are all in my box. I'd love to get feedback on any of this.
Lesson 10: Practice graphing with tables
Lesson 11: Learning to graph without tables
Posted by
Dan Wekselgreene
4
comments
![]()
Labels: algebra 1, lesson, linear functions
Monday, December 14, 2009
Review game: Trashketball
 I know that many teachers out there play some form of Trashketball, so this isn't really groundbreaking. However, I always have problems with these kinds of review games. Structuring them so that the higher-skilled students don't dominate or pressure the other students can be quite difficult. Or, looking at it the other way, there are plenty of lower-skilled students who are happy to sit back and let others on their team get the work done for them.
I know that many teachers out there play some form of Trashketball, so this isn't really groundbreaking. However, I always have problems with these kinds of review games. Structuring them so that the higher-skilled students don't dominate or pressure the other students can be quite difficult. Or, looking at it the other way, there are plenty of lower-skilled students who are happy to sit back and let others on their team get the work done for them.
I developed Tic Tac Toe Battle Royale a couple years ago which addresses some of these concerns pretty well. But you can only do the same game so many times. My experiments with Trashketball in the past haven't been that successful, and so I thought about how I could improve it to work more effectively in my class. This is what I came up with:
- Break students into groups of 3 or 4 - for me, this yields no more than 6 groups in my Algebra 1 classes. Give each group a letter, and each person in the group a number. Write these in a grid on the board. (If there is an unfilled spot in a group, that spot becomes a wild card - any person can take that number.)
- For each round, create 6 separate problems that all target the same concept, but that are slightly different. This prevents the copying problem found in board races.
- Hand out a template for doing the work on. My freshmen need an organizer for everything. "Get out a sheet of paper" just doesn't fly.
- Show the 6 versions of the problem, giving the class enough time to get it done.
- Call for silence. Block the projector. Randomly (or not) call a number between 1 and 4. The student in each group with that number comes to the board - all 6 at once. Have the board sectioned off so they know where to write. They are allowed to bring their own graphic organizer up with them, but no one on the team may offer help at this point. The idea here, of course, is that students must make sure that all group members have done the work. Students who tend to slack off have to at least write down the work that others in their group are doing. Not ideal, but it's better than spacing out.
- Have the trashketball basket set up. As students complete their work on the board, tell them if they are right or not (make sure to have answer keys ready!). Right answers get a point, and they get to take a shot for a bonus point. There is less waiting around time this way - some students will still be writing their problems as others are already lining up to shoot.
- Record the scores and move on. Winning team gets a whatever.

I did this for the first time today, and was amazed by how well they did. There were only 2 students in the class that I couldn't get totally engaged. The rest did all their work, were excited to take their shots, and so on. It takes longer to make this activity due to the multiple problems, but it was really worth it. Man, do they love tossing paper balls into the recycle bin.
I know it kind of breaks my respect class norm, but it really warms my heart to hear a kid (who I can usually barely get to sit down, and who really wanted to win) say to his teammate who hadn't done his work on the board carefully: "Fool! I told you it was negative eleven!"
Trashketball Problems (Keynote) (Powerpoint)
Answer Template (Word)
Posted by
Dan Wekselgreene
3
comments
![]()
Labels: algebra 1, fun, group work, review
Monday, November 23, 2009
Math Department Photo: 2009-2010

Michelle Longosz, our former photo teacher, always takes amazing department photos for us each year. Here is the radical math department.
Posted by
Dan Wekselgreene
7
comments
![]()
Labels: fun
Sunday, November 15, 2009
XKCD based lesson: The Coordinate Plane

Ever since I first saw this xkcd cartoon, I wanted to use it in a lesson. I finally put that together this year. I used the cartoon as a way to help convey the idea that points on a coordinate plane are a way to easily visualize the relationship between two different variables. The purpose of the numbers is simply to quantify those relationships, if such a quantification is necessary. I then had students make their own graphs for homework, with variables of their choice. If I had more time to spare, it would have been nice to do this in class (and the outcome would have been better, I think).
This lesson (Unit 4, Lesson 5) and others can be found in my box.com widget to the left. I recently updated Algebra 1, Units 3 and 4.
Here are some examples of the students' work.



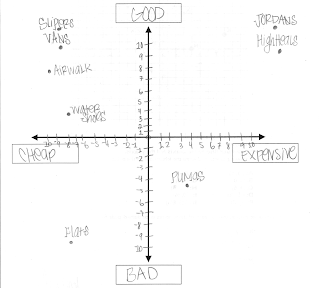

Posted by
Dan Wekselgreene
6
comments
![]()
Saturday, October 31, 2009
Story of 1

I was clued in to the existence of The Story of 1 a couple of weeks ago from my twitter PLN. I had my sub show it to my algebra 1 classes when I was out of town, and it seemed to go well. Then, one of my colleagues was sick this week and did the same lesson. Her sub said that the students were really engaged with the movie. I couldn't find a question guide on-line for it (though I didn't search all that long), so I made one up.
Posted by
Dan Wekselgreene
7
comments
![]()
Tuesday, October 27, 2009
Algebra 1: Solving Equations Puzzle

Here is a puzzle activity for reviewing equation solving. I found that it worked better when I made an answer mat for students to put their pieces onto (I indicated a couple of pieces on the mat to help them align the rest of their pieces).
Here are two files in Pages and Word that you can work from to make your own.
Edit:
A comment from David Wees in a previous post with a similar puzzle I did for quadratics:
Awesome!Yeah your puzzle is cool. So cool that I've created a random generator in Adobe Flex.
See my algebra puzzle generator.
Edit 2:
There is an app called Formulator Tarsia that will do this, but it only works for Windows (which I don't have access to) so I haven't tried it out. Give it a try!
Posted by
Dan Wekselgreene
11
comments
![]()
Labels: algebra 1, fun, puzzles, solving equations
Putting students in control of their learning
In the last couple of years, I've worked to really clarify exactly what skills I expect my students to learn. The assessment system makes it crystal clear what skills students know and don't know. And then I realized: Oh wait - it's only crystal clear to me. Students focus on their test scores, and come in to retake and improve tests, but they really don't think about what mathematical content they need to develop - only what test number they need to retake. I still have a few students who insist on retaking skills tests even though they haven't done any work to learn the skills that they got wrong the first time. Even when this fails to produce the results they want, they still resist actually working with me to learn the skill.
I think that helping students really understand what the individual skills consist of, and what their personal ability level is on each skill, is really the next step. I want students to understand the connection between their level of numeracy and their success in mastering algebraic concepts. I also want students to make connections between their behaviors in class and their growth (or lack of growth) in the lesson's objectives. Finally, I want to provide students with greater differentiation so that all students can both feel challenged and successful.
So, I put all of that together into a new plan for beginning and ending class. Students will start class with a 10 minute Do Now that has three parts. Part 1 is a Numeracy Skill Builder that targets a specific elementary math concept that is either key to the specific lesson, or something that students have been struggling with. Part 2 consists of one or two algebra concepts that are the lesson objectives. These are broken into basic, proficient, and advanced levels. The proficient level is the form in which the concept will be tested on a skills test. Students are told to solve only one problem in each concept, at the level they feel most comfortable at. Part 3 is a multiple choice test prep question. The purpose of this is obvious, as we need to get students ready for state tests, ACTs, placement tests, and so on.
Students have 10 minutes to complete these problems individually and silently. No helping is permitted here (in general), because the purpose is for students to really get a sense of what they know at the beginning of class on their own. At the end of the 10 minutes, I show the answers so students can see how they did, but we don't spend time actually reviewing these specific problems. I quickly collect the papers.
We have the lesson. Ok.
Now, in the last 5 - 7 minutes, I hand back the papers. On the back, students complete the Exit Slip / Reflection. They are supposed to go back to the Do Now problems, pick one algebra concept, and try a higher level problem. The idea is for them to see how much they can improve in an objective over the course of the class period. So, even if they are only able to accomplish the basic level (when they couldn't before), they can see growth in themselves and feel good about that. Students who already could do the advanced concepts at the beginning of the class have a shot at doing a harder challenge problem, so that they too can push their thinking (my advanced students really like this).
I just started doing this today, so I don't have too much to report about it yet. It seems to have gone well, though it took longer than the 10 minutes because I needed to explain the process a few times until they all got what I was talking about. As it becomes part of the routine, I'll know more about what impact it is really having.
Here is the first one we did, in pdf and word formats.
I'd love to get any feedback on any part of this.
Edit
We decided to make the reflection portion into a progress tracker, instead of copying it individually on the back of each Do Now. This log will be kept in a binder in the class. This will allow students to see how they did in previous classes as they are filling out the current reflection. It will also be a very useful document for discussions during grade conferences.
Posted by
Dan Wekselgreene
8
comments
![]()
Labels: algebra 1, assessment, classroom structure, differentiation
Monday, September 21, 2009
Distributive Property and Multiplying Binomials

I made a review lesson for my Algebra 2 students on these topics, to make sure they are really ready before we start performing operations on complex numbers.
Some instruction, some board races, and there you go. Hope you like it.
Lesson
Keynote
Quicktime
I also updated my Algebra 1 box with unit 2 files and the first four lessons of unit 3.
Posted by
Dan Wekselgreene
2
comments
![]()
Labels: algebra 1, algebra 2, lesson, polynomials
Saturday, September 12, 2009
Algebra 1: Solving Equations
I am beginning the planning stages of our unit on solving equations in Algebra 1. In my past experiences, some students pick this up very quickly, no matter how you teach it, while other students struggle mightily. I want to try some alternate approaches this year, to really reach those students who have not been able to learn this skill in the past. I remembered an order of operations approach that I read about in the NCTM magazine a few years back. I can't recall the name of the article, but a little google searching found me this document that is even better than what I remembered.
Our students in Numeracy already work with bar modeling to solve word problems, so this seems like a natural extension to solving equations. I like this approach because it helps focus on the idea that the variable is a given quantity that must be determined, instead of focusing on the steps that isolate the variable. It also might help with those difficult to master "converting verbal sentences to algebraic equations" problems. Here are a few examples of how this might look. I know the diagrams are a bit confusing at first, but I think they would make more sense to students as they watch them get created and do them by themselves.

I also like the other representation discussed in the article. This is the original order of operations process that I had been searching for. I like this because it gives a very clear framework for solving equations - reversing the order of operations.
When you look at each stage, you can draw equal signs between the boxes. These would be equivalent to the intermediate statements in the traditional "do the same thing to both sides" approach.
So for the unit, I am thinking that we would spend two or three lessons on bar models to build the concept of what we are actually trying to do (find the value of the unknown amount). Then, spend a couple lessons on the order of operations representation to build an understanding of the process for isolating the variable. Finally, transition to the traditional approach, which is clearly the fastest and cleanest way to solve an equation of the three. This would take more time, of course, but the hope is that it would build a more enduring understanding.
Has anyone tried these methods with their students?
Edit:
I wonder now if it would make more sense to start in with modeling sentence/word problems with the bar model method, and not start by saying that we are "solving equations". That way, more students would be engaged with the material, and we could eventually use the bar models to develop the equations.
This way, the unit doesn't start with the problem "solve (3/5)x = 45", which will stop most kids dead in their tracks, but maybe with something like "It took Sandra 45 minutes to finish 3/5 of her homework. How long will it take her to finish it all?", which kids might have more of an entry to. After we solve it, we can then discuss how to represent it as an equation.
Edit 2:
I also need to think about how to incorporate the balance idea and preserving equality... Kids don't always know what the equal sign really means. Maybe in the transition time from the box method to the traditional method?
Edit 3:
(Written on 10/27 - at the end of the unit)
On reflection, the problem was not having enough time to really devote to the two alternative methods. Both did show a lot of promise, but we weren't able to really practice either enough for it to really stick with students. The bar model method really worked to help students set up and solve word problems, so I think I will stick with that next year. Give it some more time so that it really sinks in and can be used to get a deeper understanding of fractional coefficients. I will probably save the GERMDAS method for individual tutoring with students who are not having success with the traditional balance method. Less fights... more differentiation.
All of these lessons have been added to the box widget on the left.
Posted by
Dan Wekselgreene
11
comments
![]()
Labels: algebra 1, representational fluency, solving equations
Monday, September 07, 2009
Algebra 1: Skills List
My goal for this weekend was to complete a rough draft of all the skill items that will be assessed on the first semester final exam. These items are assessed in chunks on the weekly skills tests, and in larger chunks on the 6-week benchmark exams. After each benchmark exam, the plan is to spend a lesson or two on targeted reteaching - any ideas that people have on how to make this effective would be very much appreciated.
I've finished the list, and am interested to hear what other Algebra 1 teachers think about the scope and detail of the items. What would you add? Take away?
Posted by
Dan Wekselgreene
9
comments
![]()
Labels: algebra 1, assessment, cumulative exams
Sunday, September 06, 2009
My current experience with Algeblocks
This student finished all of the simplifying expression problems on paper (correctly), and then used the algeblocks for the following:
But can I blame him? Why would a student who can already do a procedure well bother trying to figure out a slower, less portable method?
But then, the students around him who really do need to use manipulatives to help them understand the difference between 2x and x^2 don't want to use the blocks either. They feel stupid and they want to do it the faster way too.
This seems impossible without fully differentiating instruction in the classroom. Which also seems, you know, impossible.
We have our Numeracy class, in which students spend time working on ALEKS. The Numeracy teacher this year is doing small group pull-out during that time to work on specific skill building. I am starting to think we should use the manipulatives in that setting only.
Posted by
Dan Wekselgreene
3
comments
![]()
Labels: algeblocks
Saturday, September 05, 2009
Ok, I'll tweet.
I've resisted it until now, but it seems like a lot of good stuff is happening in the twitter world. No point in shutting myself out.
Posted by
Dan Wekselgreene
0
comments
![]()
Algebra 2: Error Analysis

My algebra 2 students needed more practice solving equations with rational exponents. I was trying to think of an interesting and yet still effective way for them to keep practicing, and then I thought about how the errors they make tend to be the same again and again. That reminded me that I hadn't done an error analysis activity in a long time - and just like that, the lesson was created. I assigned each table pair one problem, where they had to find the mistake, explain it, and do the work correctly. Then each pair was called to present their findings to the class; the class then worked out the problem and if they all agreed that they had found the correct solution, I allowed them to move on.
Students were generally good at finding the mistakes I had made. Will this activity help keep them from making the same mistakes in the future? We'll find out next week.
Here are the twelve problems plus homework.
Posted by
Dan Wekselgreene
3
comments
![]()
Labels: algebra 2, error analysis, exponents
Monday, August 31, 2009
Year ten at DCP, off to a strong start! My students this year rock.
Ok, so it was more than a month. But at least I'm finally writing again. I don't think I will be able to post about every lesson like I did last year, but I am still going to put my files in the box.net account for you all to look at, use, critique, etc. This year, I am reworking our Algebra 1 curriculum, so I'll be trying some new things, and hopefully be getting lots of ideas from all you other teacher bloggers. If you are reading this, and you are not blogging your ideas or posting your work online, I highly encourage you to give it a go. You will get a lot out of it, and you'll give a lot to the community.
We just finished our first unit on evaluating expressions, including order of operations and working with square roots. Up next will be simplifying expressions, and we're going to be using Algeblocks to model combining like terms and the distributive property.
Please send me feedback, especially criticism. I get lots of thanks from people for posting my work, but rarely does anyone tell me what they think would make things better. It's my tenth year, but I still have a long way to go until I'll be satisfied with my work. I need your help!
Posted by
Dan Wekselgreene
0
comments
![]()
Labels: algebra 1, collaboration, expressions, order or operations
Saturday, June 20, 2009
Back in a month
I'm going out of town for a few weeks, and with any luck, I won't be thinking about school. Posting for the new school year will start up again probably at the end of July or beginning of August. I'll be teaching Algebra 1 and Algebra 2, and will be redeveloping lots of Algebra 1 materials and posting them like I've done with Algebra 2 this past year. So come back and have a look around - I'll be looking forward to your critiques and comments.
Posted by
Dan Wekselgreene
2
comments
![]()
Thursday, May 14, 2009
Numeracy Curriculum
I finally got around to posting my old Numeracy curriculum on my box. This is by no means a final draft of what I think our 9th grade basic math support class should look like, but it is where I left it last year. I didn't decide to start using Keynote presentations until the third unit, so that's why there aren't any Keynote files in the first couple of units. This year, I am not teaching this class, so I haven't had the opportunity to keep developing these lessons. I'm sure I will get around to reworking this stuff at some point. For now, I'll throw it out there for people to look at, borrow, critique, steal, and so forth. I hope someone finds it helpful.
Posted by
Dan Wekselgreene
8
comments
![]()
Monday, May 11, 2009
Algebra 2: Quadratics
We are nearing the end of the quadratics unit, which got chopped up by the STAR test and all the associated hoopla. I don't have too much to say about it right now, except that I think it needs a good deal of revision for next year. Feel free to peruse and comment. Lesson 5 is missing because that was just a midterm review day.
Instead of linking all of the files individually, here is the folder:
I've also updated the skills tests from units 5 - 7 in the Box.
Posted by
Dan Wekselgreene
1 comments
![]()
Labels: algebra 2, lesson, quadratics
Monday, April 13, 2009
STAR Review
When we get back to school next week, we have a week of classes, and then we have the STAR tests. Instead of trying to jam in a few more concepts, we're just going to review what we've already learned, in game form. I've got "Who wants to be a millionaire?", "Tic Tac Toe Battle Royale", and "Big-L Bingo" ready to go, as well as a triage lesson (when you look at a problem, should you Guess it? Try it? Kill it?) I hope that this will yield an overall positive result. And when the test is complete, my students won't have to see another multiple choice question for the rest of the year.
Posted by
Dan Wekselgreene
2
comments
![]()
Sunday, April 05, 2009
Quick update
I haven't had much energy lately to post, but I've still been updating my box.net account. We ended unit 5 with polynomial division and we are starting unit 6 (quadratics) with completing the square. We are having our midterm before break this Friday. Over break, I'll post in more detail about some of the recent lessons. For now, feel free to download stuff from the box widget on my blog. As always, feedback on what you find there is much appreciated.
Posted by
Dan Wekselgreene
0
comments
![]()
Saturday, March 14, 2009
Algebra 1: Introduction to Inequalities

I'm not planning our Algebra 1 classes this year, so I have not been producing much for it. But I did put together a scaffolded introduction to inequalities. The objectives are for students to:
- Compare numbers using a number line (i.e. "<" means "to the left of")
- Understand the difference between open and closed circles
- Graph the solutions of a statement like "x < 3"
- Understand graphically why adding/subtracting by any number or multiplying/dividing by a positive number does not change the relative position of two numbers, while multiplying/dividing by a negative number does. In other words, students should understand when and why to "flip the inequality sign" when solving inequalities.
- Solve and graph linear inequalities
Posted by
Dan Wekselgreene
2
comments
![]()
Labels: algebra 1, lesson, linear inequalities
Friday, March 13, 2009
Algebra 2: Reducing Polynomial Fractions

I started this lesson with some theatrics. I asked them to simplify the fraction shown in the picture, and of course they all wanted to cancel the terms (as expected). I let them do it, and then changed the pretty pink heart into the fiery eruption you see here. I told them that those red slashes are like daggers through a math teacher's heart. I also told them that, when they go to college, I never ever want them to make the mistake of canceling out terms. Cancel factors, not terms! We spent a lot of time talking about the difference between factors and terms, and why this rule is true. We talked about why you can't add 5 and 5x, but you can cancel the 5's in 5/5x. I think this was time well spent, because this canceling problem is a persistent weed. From there, we practiced factoring and canceling. Pretty straightforward. In the following lesson, we multiplied and reduced products of polynomial fractions. There really were no new skills to learn, so after modeling one problem, I had them do independent practice work.
And now, I am caught up on postings!
Lesson 11 (Reducing Polynomial Fractions) doc / keynote / quicktime
Lesson 12 (Multiplying Polynomial Fractions) doc
Posted by
Dan Wekselgreene
4
comments
![]()
Algebra 2: Factoring Difference of Squares

Continuing with the lessons, we learned to factor difference of squares expressions. I used a geometric approach to help make sense out of the pattern, and it has really helped some students figure out how to more easily factor the nasty ones like 25x^2 - 16y^4. A quick sketch of the squares, labeled with their side lengths, has proven quite useful.
Lesson 9 (Difference of Squares) doc / keynote / quicktime
Lesson 10 (Review and Practice) doc / keynote / quicktime
Posted by
Dan Wekselgreene
3
comments
![]()
Algebra 2: Factoring, and More Factoring

It's been a while since I posted. The last week of February was our Junior Trip, in which we take all of our junior class on a 4-day-long trip around California to visit various CSU campuses. It's an incredibly important part of our program, because it is the time when our juniors really start to imagine themselves as college students. The tours, the student panels, seeing the dorms and classrooms, the admissions directors, and the DCP alumni all bring things into sharper focus for the 11th graders. We moved the trip earlier this year (it used to be in April) because kids come back inspired and ready to make positive changes, and so we wanted them to have more time to improve their grades before the end of the semester. It's also a great time for students and staff to bond and get to know each other in different ways. Needless to say, a 4-day, 3-night field trip with 80 high schoolers is tiring. We're all pretty much recovered now, and it's been back to business as usual. Time to catch up on some lesson postings.
In Algebra 2, we're nearing the end of the polynomials and factoring unit. I've been focusing on basic factoring techniques (look for the GCF first, then either use trinomial factoring or difference of squares, if possible). I'm still deciding whether to throw sum/difference of cubes into the mix this time around. I decided to bring simplifying and multiplying rational expressions into this unit (instead of waiting for the rationals unit) because it seemed like a good way to have them get more practice with factoring without repeating the same exact problems again and again. Plus, these questions are prominently featured on the STAR test.
One thing that has been helping students deal with factoring out the GCF is teaching them to write the prime factorization of each term in the polynomial, every time (including a -1 factor when there is a minus sign). Though it takes longer, this is pretty much a foolproof way of factoring out the GCF - many students have a lot of difficulty with the "what's the largest expression that divides into both" method.
Lesson 6 (Factoring the GCF and Trinomials) doc / keynote / quicktime
Lesson 7 (we used Algeblocks to get a better understanding of factoring trinomials) doc
Lesson 8 (Factoring Trinomials by Grouping) doc / keynote / quicktime
Posted by
Dan Wekselgreene
1 comments
![]()
Tuesday, February 10, 2009
Algebra 2: Factoring Trinomials (Part 1)

Ok, so I guess it should really be titled Algebra 1, not 2. But my students always need to review/relearn this topic. We'll go easy for the first lesson - only problems where the GCF = 1 and where the leading coefficient is 1. I made a puzzle for them to put together so that it is more fun than just doing a worksheet. I did something like this in the past with my honors class (but with much harder polynomial equations) and they really enjoyed it. That puzzle, once assembled, instructed them to do push-ups to get some candy. This one only requires that they tell me a joke - I'll add them to my arsenal if they're any good.
Lesson 5 (Factoring Trinomials 1)
Puzzle (doc / pdf)
You may also be interested in the puzzle-based Treasure Hunt I did a couple years ago in Algebra 2.
Posted by
Dan Wekselgreene
6
comments
![]()
Labels: algebra 1, algebra 2, factoring, polynomials, puzzles
Saturday, February 07, 2009
Algebra 2: Polynomials and Factoring


We just finished our first week of the second semester. The previous two weeks have been our Intersession period, where all students and teachers do totally different classes. This year, I did an algebra review class, helped organize our junior "boot camp" to help get them more ready for the college application process, and taught an anime class.
But now it's back to normal school, algebra 2, and time to start learning about polynomials. The first lesson was not that exciting, as we spent a lot of time learning all the needed vocabulary. But we also did learn about end behavior of polynomial functions, both graphically and algebraically. The next two lessons were more interesting, as we looked at the zero factor property from a graphical perspective, and then we learned how to sketch a polynomial function when given its linear factors graphically. This is scaffolding for the number line model lesson that will happen on Monday, which will allow students to solve factored form polynomial inequalities like (x - 3)(2x + 5) < 0. This isn't in the algebra 2 standards, but this kind of analysis will push them to understand functions more deeply, so I think it is worth the time.
In lesson 3, students worked as a class to generate sketches of product functions by multiplying the linear factors. They really caught on, and were able to easily get through the first problem pictured in this post. It was great to watch them work together as a class so well. The goal is that, on Monday, they will be able to understand and solve the second problem in this post.
Here are the files:
Lesson 1 (Classifying Polynomials / End Behavior) word / keynote / quicktime
Lesson 2 (Zero Factor Property) word / keynote / quicktime
Lesson 3 (Curve Sketching - Graphically) word / keynote / quicktime
Lesson 4 (Curve Sketching - Analytically) word / keynote / quicktime
Posted by
Dan Wekselgreene
1 comments
![]()
Labels: algebra 2, lesson, polynomials, representational fluency
Saturday, January 17, 2009
Do skills tests work?
As I've written about before, a large part of the students' grades this year in Algebra 2 are based off of the skills tests. The method I'm using is based of off Dan's, but I've modified it quite a bit. I'll save reflecting on the details of the method, and what should be kept/changed for the end of the year. I'm still getting a feel for the process, and what I've been doing has worked well enough that I don't want to significantly alter it until next year.
The crux of the method is that students are primarily assessed on smaller bits of information, more frequently. They are also encouraged to try and try again at the same concepts until they master them. Since students learn at different rates, and have different things going on in their lives that may prevent them from learning at a certain point in time, they can relearn and retake the skills tests whenever they want, before the end of the semester.
Instead of assessing each skill individually, I've been grouping them into clusters of 4 or 5 related skills. If a student gets, for example, the first 3 out of 5 correct, the score is 3/5. If they retake it, and get the last 4 right (but miss the first this time), I'll raise the score to 4/5, not 5/5 - even though the first one was "mastered" the first time around. This promotes lots of retaking, which is what I want, since my students really need to practice and practice in order to retain concepts.
It took students a while to understand how this system works, but as they figure it out, they love it, because it gives them a chance to really improve their grade when they fall behind. I've had a handful of students bring their grades up from Fs to Cs or Bs just in the last two to three weeks before finals, where this never would have been possible before.
My big fear, of course, is that this style of "micro-testing" would lead to artificially high grades, and that students' retention of material would not pan out. I've been eagerly anticipating the results of the final exam to get some relevant data. The final consisted of 50 questions that were compiled from the skills tests, though of course with different values. First off, here is the distribution of grades on the final exam: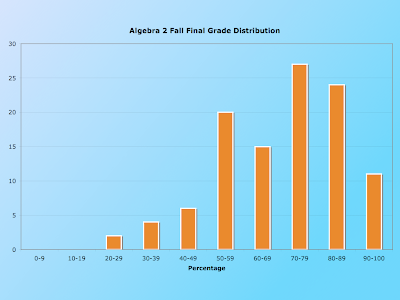
Though this may not look like something to cheer about, for a DCP final exam, this is actually quite good. The average score was a 70 and the median was a 72. But, I was more interested in thinking about the relationship between students' skills test percent and the final exam percent. If the system works as it is meant to, the skills test score should strongly predict the final exam score. The next graph shows a scatterplot of this relationship.
The purple dotted line shows what a y = x relationship would look like, and clearly (as I expected) there are more dots below the line than above - indicating students who performed better on the skills tests than on the final. But how much of a difference was there? I added in the best-fit line, and though it deviates from the purple line, it actually strikes me as not that bad. It's clear that all but a handful of students who failed the skills tests (i.e. didn't do well the first time, and didn't bother retaking them) also failed the final exam. While these students concern me greatly in terms of the task we have in motivating and educating our target students, they actually support the idea that the skills test scores are predictive of the final exam score.
The section of most concern to me is that in the red box. These are the students who had a passing score on the skills tests, but failed the final exam. Are there enough students in that section to show that the system doesn't work? I'm not really sure. Of the students who passed the skills tests, many more of them passed the final exam than did not, and I find this encouraging. And, the 24 dots in the red box all did better than 50% on the final, which means they didn't have catastrophic failure (which is not that uncommon on our final exams). But, they didn't show what we typically consider "adequate" retention, since they didn't get at least 70% of the questions right.
I'm posting this because I would like feedback and impressions from other teachers. What does the data say to you? And for those of you using a concept quiz/skills test method, what kinds of results are you seeing?
Posted by
Dan Wekselgreene
3
comments
![]()
Labels: algebra 2, assessment, cumulative exams
Wednesday, January 07, 2009
Sold out or bought in?
We're back from break, and it's time to gear up for finals. Since DCP is a California public school, my course is standards-based. I use the standards as a guideline for what to teach, but of course I must pick and choose, modify, add, and subtract in order to meet my students' needs and get them ready for higher level classes. Though it's not fun for anyone, the STAR test must be faced head-on, and I want my students to show that they really are learning math (even if it is hard to see on a day-to-day basis). To that end, I am giving a fully multiple-choice final exam. I copied the language and even the formatting of the STAR test. I feel (somewhat) justified in doing this, since none of the quizzes or cumulative exams have had any multiple choice on them. And, if they don't practice the all-or-nothing multiple choice format, they will do much worse on the STAR test (and the ACT, and the ELM, and the CAHSEE, etc.).
Most DCP students simply don't study. We do our best to teach them, but it takes a long time for students to first believe that studying helps, and then to learn how to do it effectively. On our first day back, I gave the students a practice final exam without any warning. They were not thrilled with it, but they accepted it and actually put in real effort. My purpose was to show them what their score will likely be on the final if they don't study at all. It was time well spent, because before giving them back today, I asked students to write down what percent they think they got on the test. Almost every student guessed way higher than their actual scores, and many were quite shocked. Hopefully, this will help students make wiser decisions regarding studying between now and finals (which start next Wednesday).
Here is the practice final, if you are interested.
Posted by
Dan Wekselgreene
6
comments
![]()
Labels: algebra 2, cumulative exams, STAR test


