Do skills tests work?

As I've written about before, a large part of the students' grades this year in Algebra 2 are based off of the skills tests. The method I'm using is based of off Dan's, but I've modified it quite a bit. I'll save reflecting on the details of the method, and what should be kept/changed for the end of the year. I'm still getting a feel for the process, and what I've been doing has worked well enough that I don't want to significantly alter it until next year.

The crux of the method is that students are primarily assessed on smaller bits of information, more frequently. They are also encouraged to try and try again at the same concepts until they master them. Since students learn at different rates, and have different things going on in their lives that may prevent them from learning at a certain point in time, they can relearn and retake the skills tests whenever they want, before the end of the semester.

Instead of assessing each skill individually, I've been grouping them into clusters of 4 or 5 related skills. If a student gets, for example, the first 3 out of 5 correct, the score is 3/5. If they retake it, and get the last 4 right (but miss the first this time), I'll raise the score to 4/5, not 5/5 - even though the first one was "mastered" the first time around. This promotes lots of retaking, which is what I want, since my students really need to practice and practice in order to retain concepts.

It took students a while to understand how this system works, but as they figure it out, they love it, because it gives them a chance to really improve their grade when they fall behind. I've had a handful of students bring their grades up from Fs to Cs or Bs just in the last two to three weeks before finals, where this never would have been possible before.

My big fear, of course, is that this style of "micro-testing" would lead to artificially high grades, and that students' retention of material would not pan out. I've been eagerly anticipating the results of the final exam to get some relevant data. The final consisted of 50 questions that were compiled from the skills tests, though of course with different values. First off, here is the distribution of grades on the final exam: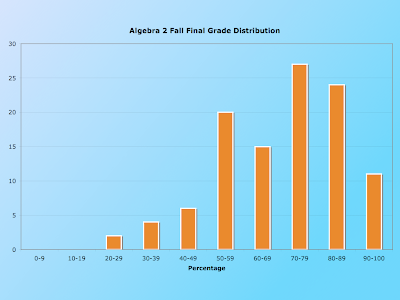



Though this may not look like something to cheer about, for a DCP final exam, this is actually quite good. The average score was a 70 and the median was a 72. But, I was more interested in thinking about the relationship between students' skills test percent and the final exam percent. If the system works as it is meant to, the skills test score should strongly predict the final exam score. The next graph shows a scatterplot of this relationship.



The purple dotted line shows what a y = x relationship would look like, and clearly (as I expected) there are more dots below the line than above - indicating students who performed better on the skills tests than on the final. But how much of a difference was there? I added in the best-fit line, and though it deviates from the purple line, it actually strikes me as not that bad. It's clear that all but a handful of students who failed the skills tests (i.e. didn't do well the first time, and didn't bother retaking them) also failed the final exam. While these students concern me greatly in terms of the task we have in motivating and educating our target students, they actually support the idea that the skills test scores are predictive of the final exam score.

The section of most concern to me is that in the red box. These are the students who had a passing score on the skills tests, but failed the final exam. Are there enough students in that section to show that the system doesn't work? I'm not really sure. Of the students who passed the skills tests, many more of them passed the final exam than did not, and I find this encouraging. And, the 24 dots in the red box all did better than 50% on the final, which means they didn't have catastrophic failure (which is not that uncommon on our final exams). But, they didn't show what we typically consider "adequate" retention, since they didn't get at least 70% of the questions right.

I'm posting this because I would like feedback and impressions from other teachers. What does the data say to you? And for those of you using a concept quiz/skills test method, what kinds of results are you seeing?