Next Lesson: Graphing Piecewise Functions

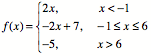
Graphing a piecewise function is one of those topics which initially doesn't seem that challenging, but I've found that students get very confused. They tend to flip back and forth between x and f(x) in their minds, and their graphs often come out totally funky. Last year, I had to backtrack and re-scaffold my lessons when I saw how tough it was. This year, I think I have a better plan.

In this lesson, after reviewing homework and warming up with more graphical analysis (see previous post), students will do more practice graphing a simple slope-intercept linear function in a restricted domain. They will do these one at a time, so they can focus on the relationship between the graph (i.e. the y-values) and the interval they are graphing on (i.e. the x-values).

Once they've got that down, I'll do some direct instruction where I show them what a piecewise function looks like, and how it can be thought of as simply putting together the restricted domain lines they were just doing into one graph. Today, we will only look at piecewise functions whose parts are constant or linear. We will go through one example together as a class, and then they will try to do one on their own.

The homework will ask them to graph two more piecewise functions, and then to do another graphical analysis problem. On that problem, they are given two linear functions f(x) and g(x), and asked to find things like f(2) * g(2) and g(4) / f(4). This is early preparation for the quadratic and rational functions units, where I ask students to graph a pair of linear functions and then point-by-point multiply (parabola) or divide (hyperbola) the y-values to create the new function. As a bonus on this homework, I am asking them to make a graph of |f(x)| and |g(x)| to see if they can connect what they know about absolute value and graphical representations to generate the v-shaped graph on their own.