Next Lesson: Solving Equations and Inequalities Graphically

This is the final lesson of the unit, aside from review and the test. The objective is for students to apply their understanding of graphical representations to be able to solve inequalities and equations.

After reviewing the homework, students will work on a Do Now worksheet with a graph of a parabola and some dotted horizontal and vertical lines. They are asked to use the graph and the lines to solve equations and inequalities.

Following this, there will be some direct instruction on solving graphically. The idea I want to present is:

To solve an equation or inequality graphically:
a) Write each side of the equation/inequality as a function
b) Graph the functions
c) Find the intersection point(s) (and draw dotted vertical “helper” lines)
d) Determine the part of the domain that solves the initial problem

We will review the absolute value problems they solved in the first unit (i.e. |x + 3| > 4), solving them graphically. I will also show them how to find points of intersection on the TI-83+. We will compare solving these graphically to solving them algebraically. Hopefully, students will see that a "less than" inequality makes a "sandwich" graph on the number line because the tip of the V is dipping below the horizontal line (does that make sense?). A "greater than" inequality makes a "gap" graph on the number line because the tops of the V go above the horizontal line to the left and right of the points of intersection.

After direct instruction, students will work independently to practice these concepts. The homework includes solving quadratic equations/inequalities in the same way. Students will also review for the third quiz (on this, plus translation and transformation of functions).

Aggressive Problem Solving

Question: "What shape will the graph of y = |mx + b| always make?"
Answer: "It'll make a fucken V shape."

I suggested to the student that, on future quizzes, he pick a different adjective to describe his graphs.

I don't know where this came from - in all my years, I've never gotten a response like that. At least he was correct, though he needs to work on his spelling.

How much is a million?

It's been a long time since I posted about the Numeracy class, mainly because I am not teaching it this year, so it's no longer at the front of my mind. But, this year's Numeracy teachers are struggling with the same concepts that I did. One of these killer concepts is rounding. This does not seem like a very difficult idea, but for our students, learning how to round a number is a huge challenge. We've tried all sorts of scaffolding, conceptual development, practice with the algorithm, and some kids just can't get it.

Ultimately, we think it comes down to a continued lack of understanding of the base-10 system. These students missed out on some very important mathematics in their first few years of school, and this is making everything else inordinately difficult for them. This week, one of the classes is piloting an activity where the students have the goal of collecting one million pennies. Each day, students will have to count how many pennies there are so far (pennies will initially be collected in a big jar). The idea is that students will eventually lose patience with this, and propose the idea of some sort of stacking or grouping. The teacher will then magically produce a container that has slots to divide the pennies into groups! When groups of 10 are no longer enough, then bigger groups of 100 will be used, and so forth.

Aside from learning more about the base-10 system, and the relative sizes of the different places, we hope that this activity will help students understand more about large numbers. We do an activity in the class where the whiteboard is divided into categories (thousands, millions, billions, trillions), and teams are given strips of paper with a quantity and a number, anad they must stick it to the board in the right column. For example, a strip might read "Number of people in San Jose (1)", or "The average income of a family of four (50)". It should come as no surprise that students usually have no idea where to put the strips of paper. In any case, this year's students seem to really doubt that there are about a million people in San Jose - they think the number is bigger by orders of magnitude. With the pennies activity, students will hopefully see that reaching a million is a bit harder than they think. But if they do reach a million, they will definitely earn their pizza party!

Next Lesson: Transforming Functions

My renewed enthusiasm for old childhood joys has come at an opportune time. In Tuesday's lesson, we will be working on transforming functions. I have a few transformers that have (incredibly) survived until now, which are currently gathering dust on my mantle. Hmm... do I bring in the opportunistic, irritating Starscream, the powerful, pea-brained Grimlock, or, everyone's favorite transforming boombox, Soundwave (though his head is broken off and I don't have any of his tape-minions).

In any case, my idea for this lesson is to have the students work on a scaffolded exploration for most of the class. They will work on learning transformations, as well as absolute value (of linear) functions. They can work individually, in pairs, or in groups, but each person must turn in their own paper by the end, and it will be graded like a quiz. The exploration/quiz is broken into 4 parts:

1) Creating absolute value functions.
In this part, students will graph a linear function. They will then graph the absolute value of the same line by looking at the y-coordinates of several points, and plotting their absolute values. They will have to then answer questions that help them see that y = |mx + b| will always make a V shape.

2) Translating absolute value functions.
In this part, students will review horizontal and vertical shifts from the previous lesson, but applied to absolute value functions.

3) Transforming absolute value functions.
In this part, students will plot out y = |x| and various transformations in the form y = a|x| to see what happens. By the end of this part, they should have a good sense for how the coefficient a affects the shape of the graph.

4) Synthesis
In the final part, students will put together what they know about translations and transformations to create the graph of f(x) = 2|x + 4| - 3. Then, they will generate a table and see if their ordered pairs fall on the graph that was created via the translation/transformation process.

After this, we will end the class with 15 - 20 minutes of direct instruction where I help formalize their understanding of transformations. I'm worried about running out of time for this. If I do, I can push it to the next class, and that will be ok, though it would be better in the same period. I hope that making the exploration into a quiz will help students focus and be more efficient with their time.

The lesson will be posted on ILoveMath.

Update:
Whoops.. I forgot that the entire sophomore class is out on a field trip to the Monterey Bay Aquarium for biology. My classes today have had about 4 people each. I got some good one-on-one time with my handful of juniors, and I'll just have to push things back to Thursday.

80's Cartoons Say it Best!

"Leadership, my sine function" - Starscream

(said derisively of Megatron's prowess as a commander)

Next Lesson: Translating Functions

Tomorrow, we will be leaving piecewise functions behind for a while. The students this year are doing better overall than last year, but some students still are having significant struggles with understanding piecewise functions. When asked to graph a single line in a restricted domain, that seems to be fine. But as soon as the pieces are put together, students get very confused between the f(x) value from the equation, and the x-values from the domain condition (I haven't graded the quiz yet, so I'll have some better information about this soon).

We'll come back to it when we review for the unit test and the final exam, but for now, we need to move on. The goal for the next lesson is for students to understand vertical and horizontal shifts - why they happen, how to determine the shift, and how to generate translated graphs.

For the Do Now, students will be asked to plot out y = x^2 and y = x^2 + 3, and compare the graphs. They will do the same for y = x^2 and y = (x - 2)^2. At this point, they are working by hand so that they can, point by point, see what is happening. We will discuss their results and get some initial conjectures out. Then, they will do a graphing calculator exploration of the same ideas, which will allow them to graph more functions more quickly.

After this, we'll put the ideas together as I do some direct instruction, and define the concepts of vertical and horizontal shift. We will use what they've learned to understand why the vertex of y = a(x - h)^2 + k is (h, k) - which is, after all, a state standard! Yes! I hope that providing more scaffolding on translations will help them understand the vertex form better. I also think it will help them be more prepared for all those crazy phase-shifting, period changing trig functions they will encounter in pre-calc (along with the upcoming lesson, which will look at stretching transformations, in general and with specific attention to absolute value functions).

Update:
I graded quiz 2 and the scores were lower than I'd hoped:
10| 0
9| 0 3 3
8| 0 3 3 3 5 8 8
7| 1 3 3 6 6 8
6| 3 6 8
5| 1 4 6
4| 4
3|
2| 0
1|

There were too many students who crashed on this one, although the bulk of the class was still in a good range. Many students had trouble with inequality notation - after working so heavily on interval notation, they seem to have forgotten how to use inequality notation, which is something they were already familiar with. For example, to express the numbers less than 3, we write (-infinity, 3) . Several students then wrote something like -infinity < x < 3 instead of just x < 3. It is always very interesting to me how new knowledge seems to crowd out old knowledge for a while, and then there is a process of assimilation where the mind brings them together and eventually sorts it out. The piecewise question was decent overall, although there are quite a few students who have not mastered it yet. I think that it needs some time to marinate in their brains, and we'll review these problems when we get toward the unit test. I think I'll develop a good error-checking handout for them to work on.

Next Lesson: Determining the function of a piecewise graph and Quiz 2

In the next class, we will start by reviewing the homework in a different manner than normal. We'll do the more traditional "I'll put the answers on the overhead, and we will go through it together to see if there are any questions" instead of my new homework review process . This is because the homework is long and has lots of short questions, and it is the review sheet for the day's quiz. I hope that reviewing the work this way today will be effective.

After the review, we will have a team challenge that is worth points on the quiz - not extra credit, but the normal, quotidian kind - 9 out of the 50 points. Teams will be given three 3-point problems, one at a time. They can work in their teams, use notes, and ask me a total of 3 questions for the whole activity. When they agree to a solution, they all sign off on that sheet and turn it in to me, getting the next problem in return. If anyone talks to a different team, they will lose 1 point from their score. I think that these rules will help keep them focused on their work and helping their teammates.

Problem 1: Given a piecewise function, make a graph

Problem 2: Given a graph of a piecewise function, determine the equations. (My hope is that they can work this out on their own, though they haven't gone in the backwards direction yet. They can use one of their 3 questions here, of course)

Problem 3: Given a graph of two lines that are not crossing, but clearly will cross, determine the exact point of intersection. (To do this, they have to determine the function of each line, and then solve the system algebraically. I think there will be a lot of confusion here, but if they ask me a good question, they should be able to proceed).

I haven't tried something like this before, so we'll see how it goes.

We'll then take a few minutes where I show them the answers and deal with any last minute questions. The class will then have the last 30 minutes to take the quiz.

The homework will focus on determining the functions of given piecewise graphs, along with review of solving absolute value inequalities and equations in preparation for the upcoming lessons in which we will solve these same problems graphically.

Next Lesson: More Piecewise Functions

This lesson will start out with students warming up on a piecewise function with only linear parts, as in the homework. The graph is followed by a series of evaluation problems. The first can be done by looking at the graph - the rest require use of the equations. This will be explained later in the class; for now, the idea is to see if students can figure out how to do it, either alone or by working together.

After reviewing this, we will add to the notes from the previous lesson. I'll show the students how to evaluate a piecewise function algebraically by determining which condition is made true by the x-value, and then substituting the x-value into the corresponding equation. We can use this idea to go back to the Do Now problems if they didn't figure them out. I will set up an x-y table to record the values we test during this portion of the lesson - next, we'll use tables to graph more complicated functions.

At this point, I'll hand out a reading to the students that shows how to use a table to help graph a piecewise function that has non-linear pieces (like absolute values, quadratics, etc.). My idea is that they will write the x-values that are the endpoints of the conditions twice in the table, and evaluate them with each of the equation parts. They will indicate on the table if the y-value is a closed or open circle. Students will then have time to practice this independently.

Homework is a set of problems that will help them review for the second quiz in the next class.

Next Lesson: Graphing Piecewise Functions

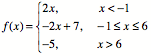
Graphing a piecewise function is one of those topics which initially doesn't seem that challenging, but I've found that students get very confused. They tend to flip back and forth between x and f(x) in their minds, and their graphs often come out totally funky. Last year, I had to backtrack and re-scaffold my lessons when I saw how tough it was. This year, I think I have a better plan.

In this lesson, after reviewing homework and warming up with more graphical analysis (see previous post), students will do more practice graphing a simple slope-intercept linear function in a restricted domain. They will do these one at a time, so they can focus on the relationship between the graph (i.e. the y-values) and the interval they are graphing on (i.e. the x-values).

Once they've got that down, I'll do some direct instruction where I show them what a piecewise function looks like, and how it can be thought of as simply putting together the restricted domain lines they were just doing into one graph. Today, we will only look at piecewise functions whose parts are constant or linear. We will go through one example together as a class, and then they will try to do one on their own.

The homework will ask them to graph two more piecewise functions, and then to do another graphical analysis problem. On that problem, they are given two linear functions f(x) and g(x), and asked to find things like f(2) * g(2) and g(4) / f(4). This is early preparation for the quadratic and rational functions units, where I ask students to graph a pair of linear functions and then point-by-point multiply (parabola) or divide (hyperbola) the y-values to create the new function. As a bonus on this homework, I am asking them to make a graph of |f(x)| and |g(x)| to see if they can connect what they know about absolute value and graphical representations to generate the v-shaped graph on their own.

Next Lesson: Domain and Range

Tomorrow, we'll start class by reviewing the homework (as always), and then I get to give students back their quiz and congratulate them on doing so well. That's always more fun for everyone than when they do poorly.

Next, students will work individually on more graphical analysis work, as in the last lesson. I'm convinced that fluidity with graphical representation is a key skill that must be continually reinforced. When I first started at DCP, I taught primarily Algebra 1. I never understood why students could graph a system of equations and find the intersection point, solve a system algebraically, but not make the connection between the point of intersection and the algebraic solution. It took me a while to see that they did not really understand the relationship between "y = 2x + 3" and the graph that they knew how to produce. Without that understanding, it becomes clear why a point of intersection seems to have nothing to do with algebra.

Anyway, following this, there will be some direct instruction where I show students a series of graphs, and help them understand how to determine the domain and range, and write them in interval and inequality notation.

Finally, there will be time for pair work practice where students will determine the domain and range of given graphs. They will also have to graph a linear function over a restricted domain. Understanding how to do this will make the upcoming piecewise functions lesson much more successful.

The homework will be practice of these concepts, with some review problems thrown in. I've been thinking about including function decomposition in the curriculum - I decided to put in some problems on this homework (shown above) where they must match a composite function with a pair of component functions as a sort of first step in that direction. We'll see how they do with it.

Update:
I've compiled six graphs with related questions that push on students' understanding of how a graph represents a function. I've uploaded them to ILoveMath in the Algebra: Misc Topics section. If you use any of my stuff, I'd love to get any feedback.

Next Lesson: Function Operations

Ok, this was actually last Friday's lesson..

We had the first quiz of the second unit. Students did well - the average score was a 79%. After this, we began exploring graphical analysis. The example shown here is part of the homework. As predicted, answering these types of questions was hard for many of the students, but we did seem to make some good progress. I didn't give them any direct instruction - just asked them to try to figure out the questions in their groups based on what they already know. Then, we reviewed the answers together. We will keep coming back to these types of problems in the upcoming lessons.

After this, I did direct instruction on adding, subtracting, and multiplying functions. Students liked this, because it only required use of their algebra 1 skills. Though the notation was different, they didn't have to learn anything "new"; the feeling of relief was almost palpable in the room.

Standards Coverage

In a comment in the previous post, Darren says:

I find the Algebra 2 standards to be fairly "aggressive", like drinking water from a fire hose. How you find time to add in topics that are not in the standards, I don't know but would be most interested in learning.

(I think it is worth starting a new post to answer this... I'm interested, as always, to hear people's thoughts.)

Well, you're right. We are not able to adequately cover all the standards as they are written, especially since our students start so far behind the curve. What we've done is to strand out the standards over the 4 years. We leave some things out of Algebra 1, and push them into Algebra 2. Some of the Algebra 2 standards we then move into Pre-Calc. And some, we decide not to do at all.

When deciding what to cover (and in what depth) in Algebra 2 Honors, I look not just at the list of state standards, but at the blueprint for the standardized test (i.e. what are the key standards that comprise the bulk of the test), at what will be covered in Geometry and Pre-Calc, and at what will be most useful for students moving in a trajectory toward Calculus.

I know we can't do it all, so my goal is to balance the required coverage with a strong scaffolding for success in Calculus - all with an eye to who our target student is.

For example, though I think conic sections is a great topic, a thorough unit would take my students many lessons to master - yet there is only one single question on the test. So we leave it for Pre-Calc.

The same is true for combinations, permutations, probability and stats, mathematical induction, series - all together these topics comprise just about 20% of the test. I choose to focus on the rest, and go deeper by including relevant scaffolding, math analysis components, word problems, and so forth.

With our students, I believe this actually yields higher test scores than covering everything more shallowly would.

Update:
There is discussion of this going on at Darren's site if you are interested.

Next Lesson: Representational Fluency

The composition lesson went fairly well, though I could have used about 5 more minutes to finish the lecture. Students seemed comfortable with finding things like f(g(2)), but I definitely lost many of them when I tried to finish with finding f(g(x)) as an expression. We'll definitely need to review this a couple of times.

In the next lesson, after reviewing the homework, the Do Now will focus on practicing these concepts (as well as reviewing absolute value inequalities).

Then, I'm going to squeeze in a mini-lesson on using the TI-83+ to graph inequalities and absolute value inequalities. In this case, I mean graphing things like y = (x < 5), where it returns 1 if true and 0 if false. This is a pretty cool way to generate a graph that looks like the number lines we shade by hand. It can solve absolute value problems the same way: y = (abs(2x+1) > 3). After learning this technique, students will check their answers from the Do Now by graphing. I'm hoping that this doesn't take too much time...

Finally, I will give students a handout on Representational Fluency. I've learned from my experiences teaching AP Calculus in previous years how important it is for students to be able to move comfortably between equations, graphs, tables, verbal descriptions, arrow mappings, etc - especially when it comes to the concept of functions. This sheet focuses on graph and table representations of functions - students have to figure out things like f(2) and f(g(-2)) from these representations. I'll post this on ILoveMath .

Update:
I'm trying to decide if I should do some work on function decomposition. This is clearly a skill that students will need for Calculus (i.e. working with the chain rule). I also think that decomposing functions might help them understand better what composing functions really means. But I'm also worried about overloading them, and I wonder if they need more time to digest function notation and composition first. It's not in the standards, as far as I can tell, so I wonder if students are expected to understand this idea before getting to Calculus. Any ideas?

Next Lesson: Function Composition

Up next, students will learn to evaluate composite functions. First, they will do a worksheet with function notation practice problems. I set the problems up in groups of 4 as follows: f(2), f(-4), f(a), f(2x - 5). I think that sneaking up this way on the idea of plugging in an expression for x will help students better understand how to evaluate f(g(x)) as an expression. I remember having a lot of difficulty when I first learned this concept, and this method helps make it clearer for me anyway...

Then, we'll use this dual lens model. I hope it will help them visualize what "the output of f is the input of g" means. After the model, we'll go through the concept of composing functions, and do some example problems together.

In an upcoming class, I will give students a chance to do function composition when given graphs or tables instead of equations.