Algebra 1: Skills List

My goal for this weekend was to complete a rough draft of all the skill items that will be assessed on the first semester final exam. These items are assessed in chunks on the weekly skills tests, and in larger chunks on the 6-week benchmark exams. After each benchmark exam, the plan is to spend a lesson or two on targeted reteaching - any ideas that people have on how to make this effective would be very much appreciated.

I've finished the list, and am interested to hear what other Algebra 1 teachers think about the scope and detail of the items. What would you add? Take away?

Do skills tests work?

As I've written about before, a large part of the students' grades this year in Algebra 2 are based off of the skills tests. The method I'm using is based of off Dan's, but I've modified it quite a bit. I'll save reflecting on the details of the method, and what should be kept/changed for the end of the year. I'm still getting a feel for the process, and what I've been doing has worked well enough that I don't want to significantly alter it until next year.

The crux of the method is that students are primarily assessed on smaller bits of information, more frequently. They are also encouraged to try and try again at the same concepts until they master them. Since students learn at different rates, and have different things going on in their lives that may prevent them from learning at a certain point in time, they can relearn and retake the skills tests whenever they want, before the end of the semester.

Instead of assessing each skill individually, I've been grouping them into clusters of 4 or 5 related skills. If a student gets, for example, the first 3 out of 5 correct, the score is 3/5. If they retake it, and get the last 4 right (but miss the first this time), I'll raise the score to 4/5, not 5/5 - even though the first one was "mastered" the first time around. This promotes lots of retaking, which is what I want, since my students really need to practice and practice in order to retain concepts.

It took students a while to understand how this system works, but as they figure it out, they love it, because it gives them a chance to really improve their grade when they fall behind. I've had a handful of students bring their grades up from Fs to Cs or Bs just in the last two to three weeks before finals, where this never would have been possible before.

My big fear, of course, is that this style of "micro-testing" would lead to artificially high grades, and that students' retention of material would not pan out. I've been eagerly anticipating the results of the final exam to get some relevant data. The final consisted of 50 questions that were compiled from the skills tests, though of course with different values. First off, here is the distribution of grades on the final exam: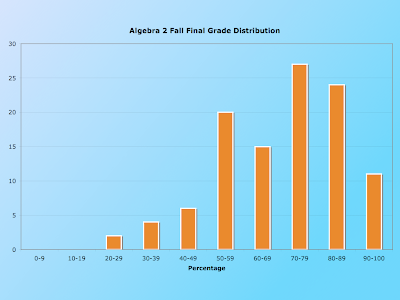



Though this may not look like something to cheer about, for a DCP final exam, this is actually quite good. The average score was a 70 and the median was a 72. But, I was more interested in thinking about the relationship between students' skills test percent and the final exam percent. If the system works as it is meant to, the skills test score should strongly predict the final exam score. The next graph shows a scatterplot of this relationship.



The purple dotted line shows what a y = x relationship would look like, and clearly (as I expected) there are more dots below the line than above - indicating students who performed better on the skills tests than on the final. But how much of a difference was there? I added in the best-fit line, and though it deviates from the purple line, it actually strikes me as not that bad. It's clear that all but a handful of students who failed the skills tests (i.e. didn't do well the first time, and didn't bother retaking them) also failed the final exam. While these students concern me greatly in terms of the task we have in motivating and educating our target students, they actually support the idea that the skills test scores are predictive of the final exam score.

The section of most concern to me is that in the red box. These are the students who had a passing score on the skills tests, but failed the final exam. Are there enough students in that section to show that the system doesn't work? I'm not really sure. Of the students who passed the skills tests, many more of them passed the final exam than did not, and I find this encouraging. And, the 24 dots in the red box all did better than 50% on the final, which means they didn't have catastrophic failure (which is not that uncommon on our final exams). But, they didn't show what we typically consider "adequate" retention, since they didn't get at least 70% of the questions right.

I'm posting this because I would like feedback and impressions from other teachers. What does the data say to you? And for those of you using a concept quiz/skills test method, what kinds of results are you seeing?

Sold out or bought in?

We're back from break, and it's time to gear up for finals. Since DCP is a California public school, my course is standards-based. I use the standards as a guideline for what to teach, but of course I must pick and choose, modify, add, and subtract in order to meet my students' needs and get them ready for higher level classes. Though it's not fun for anyone, the STAR test must be faced head-on, and I want my students to show that they really are learning math (even if it is hard to see on a day-to-day basis). To that end, I am giving a fully multiple-choice final exam. I copied the language and even the formatting of the STAR test. I feel (somewhat) justified in doing this, since none of the quizzes or cumulative exams have had any multiple choice on them. And, if they don't practice the all-or-nothing multiple choice format, they will do much worse on the STAR test (and the ACT, and the ELM, and the CAHSEE, etc.).

Most DCP students simply don't study. We do our best to teach them, but it takes a long time for students to first believe that studying helps, and then to learn how to do it effectively. On our first day back, I gave the students a practice final exam without any warning. They were not thrilled with it, but they accepted it and actually put in real effort. My purpose was to show them what their score will likely be on the final if they don't study at all. It was time well spent, because before giving them back today, I asked students to write down what percent they think they got on the test. Almost every student guessed way higher than their actual scores, and many were quite shocked. Hopefully, this will help students make wiser decisions regarding studying between now and finals (which start next Wednesday).

Here is the practice final, if you are interested.

Newsflash: Students Don't Study

The results from my first Algebra 2 comprehensive test were (predictably) bad. Though they were even worse than I was anticipating. The test included a reflection that asked students, among other things, if they felt that they were well prepared for the test. Most of them were honest and said that they didn't really study. I gave students the option to create and use a 1-page study sheet for the test; less than half of them bothered to do this. It's an ongoing battle trying to get students to see and believe that there is a connection between their actions and the grades that they receive. Many students wrote that they thought they would be able to pass the test without studying. I hope that this is a wake-up call for them. I know that they want to succeed in the class - I have to do a better job of teaching them how to study and convincing them that studying actually has a purpose.

Radical Butterflies from Hell

We used to have our fall finals at the end of December, right before the students went on break. In the past couple of years, we have moved them to after break in order to keep the same schedule as the rest of the schools in our district. This has both positive and negative effects, the latter obviously being that two weeks of vacation tends to sap the content knowledge out of even the most diligent students' brains. Most teachers spend the first week back reviewing everything, since finals happen Tuesday through Thursday of the second week (this coming Tuesday is my Algebra 2 final).

To make it a little more fun for my class, I decided to hold the First Annual DCP Algebra 2 Honors Fall Final Review Math Olympics, and I told them that the ceremony for the bronze, silver, and gold winners will be nationally televised (I'm still tring to come up with the prizes. I wonder, if I take them off campus for lunch, is that a prize or a punishment? Please leave a comment if you can think of any good prizes that 10th graders might enjoy!). The students are in teams of three and needed to come up with a team name using a type of number, along with a place to represent in the games. We have, for example, the Imaginary Mathematicians from New York City, the Radical Mexicans from Michoacan, and the Radical Butterflies from Hell; the Real X-tremes from Hawaii are currently in the lead. Each day this week, there was a series of events to review key concepts, and each homework was a set of multiple choice STAR-type problems that counted as additional events.

Today (Saturday), we had a terrific review session. I told students I would be at school at 10:30, and many were there by 10:15. I had most of the class show up (only about 5 or 6 didn't), and they stayed until after 2:00, ordering pizza for lunch. We pushed the tables together into one big conference table, and they all sat around it, going over old tests, doing their homework, working together, and asking me questions. I really need to recognize the whole class at our next school assembly for such high quality effort, work, and behavior. I'm proud of how they're coming together as a class; I hope (now more than ever) that they all pass the final.

I'm more afraid of the midterm than they are...

Tomorrow is the fall midterm for my Algebra 2 Honors class. It covers everything from the start of the year: the real number system and its properties, solving equations with rational coefficients, everything about functions and graphical analysis, systems of linear and non-linear inequalities, and 3x3 systems of equations. That's quite a large chunk of material for anyone, let alone students who were below grade level less than 2 years ago.

DCP students are notorious for being able to do well in the short term, but completely falling apart in the long term (>3 weeks or so). Traditionaly, the majority of a class will get a C or an F (no Ds at DCP!) on a midterm or final, even if they had been doing well all along. We haven't figured out yet how to help them do better on large cumulative exams. Sometimes it feels like their brains are a cup that can hold a fixed amount of liquid - as soon as you pour more in, the rest splashes out to make room. For this reason, final exams are only 10% of the class grade in all freshmen classes, and it goes up by 5% a year. We need our seniors to be prepared to take college classes where the final is 25 - 30% (or even more) of the grade, and to understand how significant that is.

I don't know if their retention problems mean that they did not really understand the material in the first place, or if it means that they still don't really understand how to study (or how you need to study differently for this kind of exam), or if there is something else going on. I was helping a student review today, who admittedly has been struggling to do well, but usually has a pretty good sense of what's going on. He got confused on a problem, so I posed a simpler problem (or so I thought...) to try and help him understand. I wrote on the board: if f(x) = x + 2, what is f(3)? He looked at me like he had no idea what I was talking about. Honestly, I am amazed by this. I have no way to explain why he couldn't answer that question. I do have one observation: when students are struggling with one difficult concept, they seem to be unable to access previously learned concepts at the same time, even if they could use that concept well in a different context. Maybe it's like being able to toss and catch different objects individually with no problem, but dropping them all when trying to juggle.

It makes sense to me that students would forget complex formulas or methods over time - this happens to me too. But, if they learned them properly, a little bit of review should bring them right back. However, when students don't recall foundational concepts (I had a calculus student once ask me, while studying for the final, what a derivative was), I don't know how to help them, except to implore them to see me for as much extra help as possible.

So, we'll see tomorrow how it goes. I'm predicting a bloodbath, but I hope they'll defy the trends. If anyone has ideas about how to better prepare students for cumulative tests, please share them in the comments section.

Update:
Here are the scores:

10| 2
9| 7
8| 0 1 5 8 8
7| 1 2 2 2 4 4
6| 2 5 7 8
5| 2 4 5
4| 9
3|
2|
1|

Well, as predicted, the scores were much lower than a typical unit test. At least the majority of the class still passed, and my top student is still getting over 100%! She's an algebra machine.