Next Lesson: Systems of Inequalities

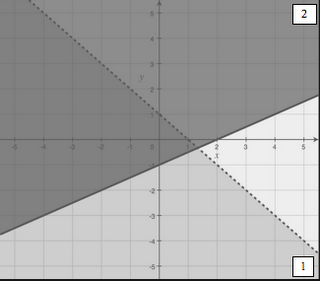
In this lesson, we will go beyond graphing linear inequalities to graphing systems of inequalities, including non-linear inequalities (we'll use absolute value and quadratic equations, as those as the non-linear functions we practiced in the last unit).

Just like in the last lesson, we'll start with a visual activity. Students are given a graph of a system of inequalities, with the two inequalities labeled "1" and "2". They are given a bunch of points, and must determine if the point satisfies the first, the second, both, or neither, and then plot out a "1", "2", "B", or "N" at the coordinates. I want them to not just know that the overlapping region is the solution, but to be able to identify which inequality in the system is not satisfied by a given non-solution point.

At this point, there will be some direct instruction on how to graph a system of inequalities, and reinforcement that the overlapping region is the set of all points that satisfies all inequalities in the system. I will also show them how to graph non-linear inequalities by graphing the "border function" (paying attention to whether it is a solid or dashed line), and then plugging in a test point to determine which region to shade.

After this, students will work independently to practice. I think these will be a bit tough for them because each problem has a little wrinkle in it. I didn't want to give them a bunch of simple lines - that wouldn't be any fun! We'll see how they do. I hope they get it, because I want to move on to the next topic in the following lesson and not spend much time reviewing.

The lesson will be posted at ILoveMath.org.